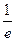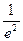题目内容
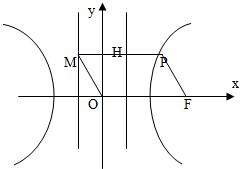
如图,F为双曲线C:
-
=1(a>0,b>0)的右焦点.P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点.已知四边形OFPM为平行四边形,|PF|=λ|OF|.
(Ⅰ)写出双曲线C的离心率e与λ的关系式;
(Ⅱ)当λ=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若|AB|=12,求此时的双曲线方程.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)写出双曲线C的离心率e与λ的关系式;
(Ⅱ)当λ=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若|AB|=12,求此时的双曲线方程.

(Ⅰ)∵四边形OFPM是平行四边形,
∴|OF|=|PM|=c,作双曲线的右准线交PM于H,则|PM|=|PH|+2×
,
又e=
=
=
=
=
,e2-λe-2=0.
(Ⅱ)当λ=1时,e=2,|PF|=|OF|.
∴c=2a,b2=3a2,双曲线为
-
=1且平行四边形OFPM是菱形,
由图象,作PD⊥X轴于D,则直线OP的斜率为
=
=
,则直线AB的方程为y=
(x-2a),代入到双曲线方程得:
4x2+20ax-29a2=0,又|AB|=12,
由|AB|=
,
得:12=
,
解得a=1,
则b2=3,
所以x2-
=1为所求.
∴|OF|=|PM|=c,作双曲线的右准线交PM于H,则|PM|=|PH|+2×
| a2 |
| c |
又e=
| |PF| |
| |PH| |
| λ|OF| | ||
c-2
|
| λc | ||
c-2
|
| λc2 |
| c2-2a2 |
| λe2 |
| e2-2 |
(Ⅱ)当λ=1时,e=2,|PF|=|OF|.
∴c=2a,b2=3a2,双曲线为
| x2 |
| a2 |
| y2 |
| 3a2 |
由图象,作PD⊥X轴于D,则直线OP的斜率为
| PD |
| OD |
| ||||
c-
|
| ||
| 3 |
| ||
| 3 |
4x2+20ax-29a2=0,又|AB|=12,
由|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
得:12=
|
(5a)2+4×
|
解得a=1,
则b2=3,
所以x2-
| y2 |
| 3 |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
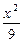 -
-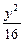 =1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________.
=1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________.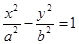 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是
的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是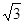
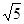
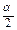 等于( )
等于( )