题目内容
(08年湖北卷理)(本小题满分13分)
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,
∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.
若△OEF的面积不小于2![]() ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.

(1)解法1:以![]() 为原点,
为原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则![]() ,
,
由题意得![]() 。
。
所以曲线![]() 是以原点为中心,
是以原点为中心,![]() 、
、![]() 为焦点的双曲线。
为焦点的双曲线。
设实半轴长为![]() ,虚半轴长为
,虚半轴长为![]() ,半焦距为
,半焦距为![]() ,
,
则![]()
所以曲线![]() 的方程为
的方程为![]() 。
。
解法2:同解法1建立平面直角坐标系,则由题意可得
![]()
所以曲线![]() 是以原点为中心,
是以原点为中心,![]() 、
、![]() 为焦点的双曲线。
为焦点的双曲线。
设双曲线的方程为![]()
则由 解得
解得![]() ,
,
所以曲线![]() 的方程为
的方程为![]() 。
。

(2)解法1:由题意,可设直线![]() 的方程为
的方程为![]() ,代入双曲线
,代入双曲线![]() 的方程并整理得
的方程并整理得
![]() ……①
……①
因为与双曲线相交不同的两点E、F,

![]() ……②
……②
设![]() 则由①式得
则由①式得![]() ,于是
,于是
 .
.
而原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,

若![]() 面积不小于
面积不小于![]() ,即
,即![]() ,则有
,则有 ,
,
解得![]() ……③
……③
综合②、③知,直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.
解法2:由题意,可设直线![]() 的方程为
的方程为![]() ,代入双曲线
,代入双曲线![]() 的方程并整理得
的方程并整理得
![]() 因为与双曲线相交不同的两点E、F,
因为与双曲线相交不同的两点E、F,

![]() ……②
……②
设![]() 则由①式得
则由①式得 ……③
……③
当E、F在同一支上时,
![]()
当E、F在不同一支上时,
![]()
综上得![]() ,于是由
,于是由![]() 及③式,得
及③式,得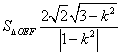 。
。
若![]() 面积不小于
面积不小于![]() ,即
,即![]() ,则有
,则有 ,
,
解得![]() ……④
……④
综合②、④知,直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.
【试题解析】本题条件涉及到一动点到两定点距离差的绝对值,容易想到双曲线的定义,所以第(1)问只要求求了出双曲线方程中的![]() 与
与![]() 。第(2)涉及到直线与圆锥曲线相交的问题,一般是要设出直线联立曲线,再用韦达定理,本问要解法的是求范围的问题,其不等式在第(2)问中已给出,所以只需写出三角形面积的表达式。
。第(2)涉及到直线与圆锥曲线相交的问题,一般是要设出直线联立曲线,再用韦达定理,本问要解法的是求范围的问题,其不等式在第(2)问中已给出,所以只需写出三角形面积的表达式。
【高考考点】本题考查直线、圆和双曲线等平面几何的基础知识,考查轨迹方程的求法、不等式的解法以及综合解题能力和运算能力。
【易错提醒】直线与双曲线有两个交点时,在联立后的一元二次方程的二次项系数不能为零,再就是解不等式后,结果是取交集还是并集,那些地方要带等号那些地方不带等号,这些都考生容量出错的地方。
【备考提示】要牢记圆锥曲线的定义,并会灵活运用;不等式的解法要熟练掌握。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

