题目内容
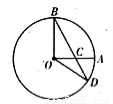
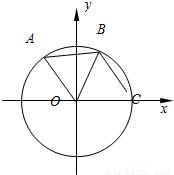
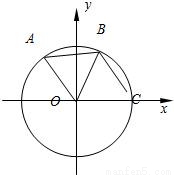
如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.(1)求cos∠COA;
(2)求|BC|的值.
【答案】分析:(1)求cos∠COA,由图与题设知知终边一点的坐标为(-3,4),故可求出该点到原点的距离,用定义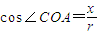 求出余弦值.
求出余弦值.
(2)由题设知∠BOC=∠COA-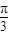 ,由(1)中可以求出∠COA正弦与余弦,然后用两角差的余弦公式求
,由(1)中可以求出∠COA正弦与余弦,然后用两角差的余弦公式求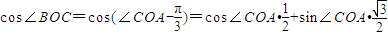 的值,再由余弦定理,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC求出BC的长度.
的值,再由余弦定理,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC求出BC的长度.
解答:解:(1)由题意可知:x=-3,y=4,且圆半径r=|OA|=5,
根据三角函数定义可得:
(2)在△OBC中,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC=25+25-50•cos∠BOC
∵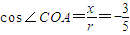 ,
,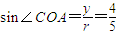
∴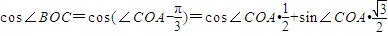 =
=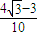
∴
∴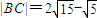
点评:本题考点是三角函数的定义,考查了用三角函数的定义---知终边上一点的坐标求三角函数值,以及利用余弦定理求边,用两角和与差的三角函数公式求角的三角函数值.
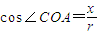 求出余弦值.
求出余弦值.(2)由题设知∠BOC=∠COA-
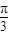 ,由(1)中可以求出∠COA正弦与余弦,然后用两角差的余弦公式求
,由(1)中可以求出∠COA正弦与余弦,然后用两角差的余弦公式求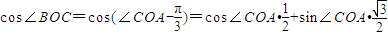 的值,再由余弦定理,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC求出BC的长度.
的值,再由余弦定理,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC求出BC的长度.解答:解:(1)由题意可知:x=-3,y=4,且圆半径r=|OA|=5,
根据三角函数定义可得:

(2)在△OBC中,|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC=25+25-50•cos∠BOC
∵
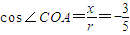 ,
,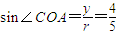
∴
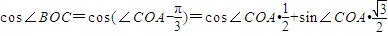 =
=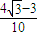
∴

∴
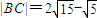
点评:本题考点是三角函数的定义,考查了用三角函数的定义---知终边上一点的坐标求三角函数值,以及利用余弦定理求边,用两角和与差的三角函数公式求角的三角函数值.

练习册系列答案
相关题目
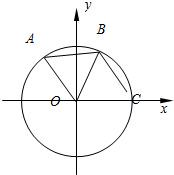 如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.
如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.