题目内容
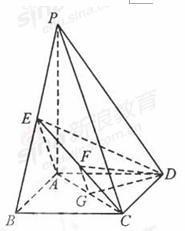
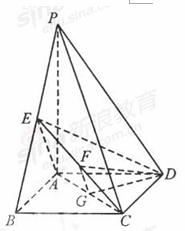
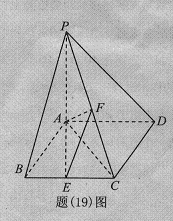
如题(19)图,四棱锥P- ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠ABC= 60°,直线PC与底面ABCD所成的角为45°,E、F分别是BC、PC的中点.
(I)证明:AE⊥PD;
(II)求二面角E—AF—C的余弦值,
解:(Ⅰ)![]()
![]() ……………6分
……………6分
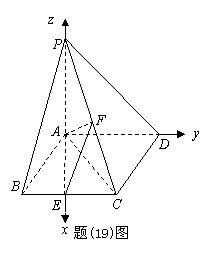
(Ⅱ)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
设菱形![]() 的边长为
的边长为![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]()
 设平面
设平面![]() 的法向量为
的法向量为![]()
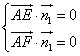
![]()
![]()
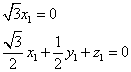
令![]() 得
得 ![]()
同理可得平面![]() 的法向量
的法向量![]()
∴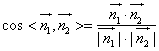
![]()
∴二面角![]() 的余弦值为
的余弦值为![]() ……………13分
……………13分

练习册系列答案
相关题目
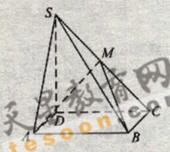
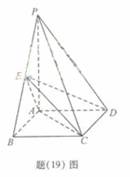 如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,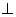 底面ABCD,PA=AB=
底面ABCD,PA=AB=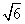 ,点E是棱PB的中点。
,点E是棱PB的中点。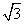 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。