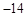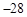题目内容
二项式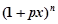 (
(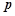 为大于零的常数)的展开式中各项的二项式系数之和为1024,按
为大于零的常数)的展开式中各项的二项式系数之和为1024,按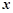 的升幂排列的前三项的系数之和是201.
的升幂排列的前三项的系数之和是201.
(1)求常数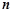 和
和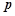 ;
;
(2)求该二项展开式中含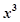 项的系数.
项的系数.
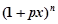 (
(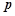 为大于零的常数)的展开式中各项的二项式系数之和为1024,按
为大于零的常数)的展开式中各项的二项式系数之和为1024,按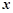 的升幂排列的前三项的系数之和是201.
的升幂排列的前三项的系数之和是201.(1)求常数
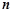 和
和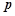 ;
; (2)求该二项展开式中含
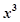 项的系数.
项的系数.解:(1)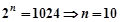 。。。。。。。1分
。。。。。。。1分
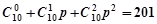
得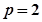 或
或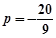 (舍去),
(舍去),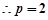 。。。。。。。。3分
。。。。。。。。3分
(2)设含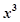 项为
项为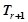 , 则
, 则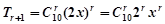 。。。。。。。。4分
。。。。。。。。4分
令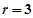 ,得含
,得含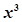 项的系数为
项的系数为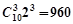 。。。。。。。6分
。。。。。。。6分
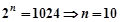 。。。。。。。1分
。。。。。。。1分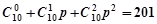
得
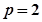 或
或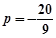 (舍去),
(舍去),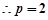 。。。。。。。。3分
。。。。。。。。3分(2)设含
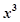 项为
项为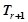 , 则
, 则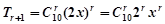 。。。。。。。。4分
。。。。。。。。4分令
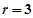 ,得含
,得含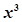 项的系数为
项的系数为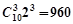 。。。。。。。6分
。。。。。。。6分本试题主要考查了二项式定理的运用,求解二项式系数的和以及数列通项公式的运用。
(1)因为二项式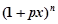 (
(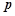 为大于零的常数)的展开式中各项的二项式系数之和为1024,则
为大于零的常数)的展开式中各项的二项式系数之和为1024,则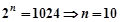 ,又因为按
,又因为按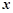 的升幂排列的前三项的系数之和是201.可知p的值。
的升幂排列的前三项的系数之和是201.可知p的值。
(2)设含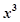 项为
项为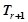 , 则
, 则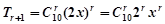
令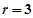 ,得含
,得含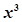 项的系数的值。
项的系数的值。
(1)因为二项式
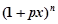 (
(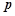 为大于零的常数)的展开式中各项的二项式系数之和为1024,则
为大于零的常数)的展开式中各项的二项式系数之和为1024,则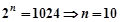 ,又因为按
,又因为按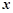 的升幂排列的前三项的系数之和是201.可知p的值。
的升幂排列的前三项的系数之和是201.可知p的值。(2)设含
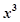 项为
项为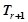 , 则
, 则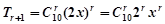
令
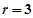 ,得含
,得含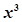 项的系数的值。
项的系数的值。
练习册系列答案
相关题目

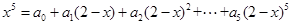 ,那么
,那么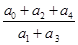 的值为( )
的值为( )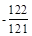 B:-
B:-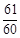 C:-
C:-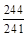 D:-1
D:-1 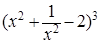 的展开式中常数项是( )
的展开式中常数项是( )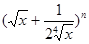
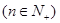 展开式中前三项系数成等差数列.
展开式中前三项系数成等差数列.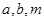 为正整数,若
为正整数,若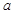 和
和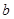 除以
除以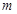 的余数相同,则称
的余数相同,则称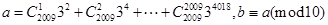 ,则
,则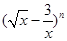 的展开式中,第4项为常数项
的展开式中,第4项为常数项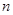 的值; (2) 求展开式中含
的值; (2) 求展开式中含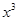 项系数.
项系数.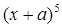 的展开式中
的展开式中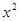 的系数为80,则a= .
的系数为80,则a= .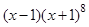 的展开式中x5的系数是( )
的展开式中x5的系数是( )