题目内容
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 时,
时, 的解析式为______,不等式
的解析式为______,不等式 的解集为________.
的解集为________.
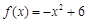 ;
;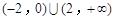
解析试题分析: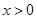 时,
时, ,所以
,所以 ,因为函数
,因为函数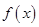 是定义在
是定义在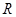 上的奇函数,所以
上的奇函数,所以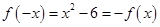 ,所以
,所以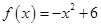 ,即
,即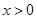 时
时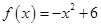 。当
。当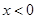 时,
时,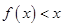 即
即 ,解得
,解得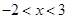 ,又因为
,又因为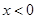 ,所以
,所以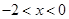 ;当
;当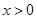 时,
时,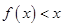 即
即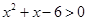 ,解得
,解得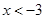 或
或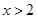 ,又因为
,又因为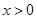 ,所以
,所以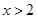 ,综上可得
,综上可得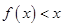 的解集是
的解集是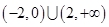 。
。
考点:1函数的奇偶性;2一元二次不等式;3分类讨论思想。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
下列函数中,既是奇函数又在区间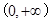 上单调递增的函数为( )
上单调递增的函数为( )
A.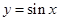 | B.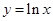 | C.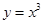 | D. |
已知函数 与
与 的图像在
的图像在 上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )
上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
己知集合M={﹣1,1,2,4}N={0,1,2}给出下列四个对应法则,其中能构成从M到N的函数是( )
| A.y=x2 | B.y=x+1 | C.y=2x | D.y=log2|x| |
函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=( )
| A.ex+1 | B.ex﹣1 | C.e﹣x+1 | D.e﹣x﹣1 |
若 ,则函数
,则函数 的两个零点分别位于区间( )
的两个零点分别位于区间( )
| A.(a,b)和(b,c)内 |
| B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 |
| D.(-∞,a)和(c,+∞)内 |
函数 的定义域为( )
的定义域为( )
A.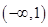 |
B. |
C. |
D.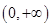 |
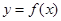 对任意的x满足
对任意的x满足  ,当-l≤x<l时,
,当-l≤x<l时, .函数
.函数  若函数在
若函数在  上有6个零点,则实数a的取值范围是( )
上有6个零点,则实数a的取值范围是( )



 的图象为
的图象为