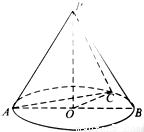
题目内容
 如图所示,在圆锥PO中,已知PO=
如图所示,在圆锥PO中,已知PO=| 2 |
| ||
| 3 |
| ||
| 3 |
分析:过点C作CD⊥AB,垂足为D,过点D作DF⊥PA,垂足为F,连接CF,可证∠CFD为二面角B-PA-C的平面角,求出DF=
,CF=
=
,即可求得二面角B-PA-C的余弦值.
| ||
| 2 |
|
| 3 |
| 2 |
解答: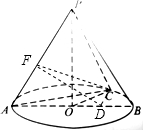 解:过点C作CD⊥AB,垂足为D,过点D作DF⊥PA,垂足为F,连接CF,则
解:过点C作CD⊥AB,垂足为D,过点D作DF⊥PA,垂足为F,连接CF,则
∵PO⊥圆O,CD?圆O,∴PO⊥CD
∵AB∩PO=O,∴CD⊥平面PAB
∵DF⊥PA,∴CF⊥PA
∴∠CFD为二面角B-PA-C的平面角
∵⊙O的直径AB=2,点C在弧AB上,且∠COB=60°
∴CD=
,AD=
∵PO=
,∴PA=
由AD×PO=PA×DF,可得DF=
∴CF=
=
∴cos∠CFD=
=
故答案为:
 解:过点C作CD⊥AB,垂足为D,过点D作DF⊥PA,垂足为F,连接CF,则
解:过点C作CD⊥AB,垂足为D,过点D作DF⊥PA,垂足为F,连接CF,则∵PO⊥圆O,CD?圆O,∴PO⊥CD
∵AB∩PO=O,∴CD⊥平面PAB
∵DF⊥PA,∴CF⊥PA
∴∠CFD为二面角B-PA-C的平面角
∵⊙O的直径AB=2,点C在弧AB上,且∠COB=60°
∴CD=
| ||
| 2 |
| 3 |
| 2 |
∵PO=
| 2 |
| 3 |
由AD×PO=PA×DF,可得DF=
| ||
| 2 |
∴CF=
|
| 3 |
| 2 |
∴cos∠CFD=
| DF |
| CF |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查二面角的平面角,解题的关键是正确作出二面角的平面角,利用等面积计算DF的长,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
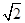 ,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
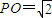 ,⊙O的直径AB=2,点C在弧AB上,且∠COB=60°,则二面角B-PA-C的余弦值是 .
,⊙O的直径AB=2,点C在弧AB上,且∠COB=60°,则二面角B-PA-C的余弦值是 .