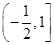题目内容
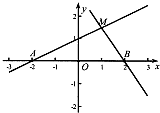 如图,A,B两点的坐标分别为(-2,0),(2,0),直线AM,BM相交于点M,且它们的斜率之积是
如图,A,B两点的坐标分别为(-2,0),(2,0),直线AM,BM相交于点M,且它们的斜率之积是| 3 |
| 4 |
(1)求点M的轨迹C的方程;
( 2)是否存在斜率为l直线l与曲线C交于P,Q两点,且使△OPQ的面积等于
| 12 |
| 7 |
分析:(1)设出M的坐标,利用直线AM,BM的斜率之积是
,建立方程,即可得到点M的轨迹C的方程;
(2)设出直线方程代入椭圆方程,利用韦达定理及△OPQ的面积等于
,建立方程,即可求得结论.
| 3 |
| 4 |
(2)设出直线方程代入椭圆方程,利用韦达定理及△OPQ的面积等于
| 12 |
| 7 |
解答:解:(1)设M(x,y),则由条件可得
•
=-
整理可得
+
=1(x≠±2);
(2)假设存在满足条件的直线l,其方程为y=x+m,设P(x1,y1),Q(x2,y2)
直线方程代入椭圆方程,消去y可得7x2+8mx+4m2-12=0
∴x1+x2=-
,x1x2=
由△=64m2-28(4m2-12)>0可得m2<7
∴|PQ|=
=
×
∵圆的O到直线l的距离d=
∴
×
×
×
=
∴m=±
或m=±2,满足m2<7
∴存在满足条件的直线l,其方程为y=x±
或y=x±2.
| y |
| x+2 |
| y |
| x-2 |
| 3 |
| 4 |
整理可得
| x2 |
| 4 |
| y2 |
| 3 |
(2)假设存在满足条件的直线l,其方程为y=x+m,设P(x1,y1),Q(x2,y2)
直线方程代入椭圆方程,消去y可得7x2+8mx+4m2-12=0
∴x1+x2=-
| 8m |
| 7 |
| 4m2-12 |
| 7 |
由△=64m2-28(4m2-12)>0可得m2<7
∴|PQ|=
| 2(x1-x2)2 |
4
| ||
| 7 |
| 21-3m2 |
∵圆的O到直线l的距离d=
| |m| | ||
|
∴
| 1 |
| 2 |
4
| ||
| 7 |
| 21-3m2 |
| |m| | ||
|
| 12 |
| 7 |
∴m=±
| 3 |
∴存在满足条件的直线l,其方程为y=x±
| 3 |
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2013•温州二模)如图.直线l:y=kx+1与椭圆C1:
(2013•温州二模)如图.直线l:y=kx+1与椭圆C1: 是单位圆和
是单位圆和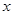 轴正半轴的交点,
轴正半轴的交点,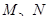 是单位圆上的两点,
是单位圆上的两点,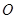 是坐
是坐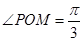 ,
,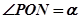 ,
,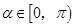 ,
,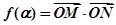 ,则
,则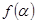 的范围为 ( )
的范围为 ( )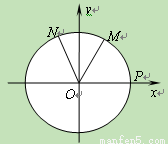
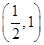 (B)
(B) 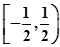 .(C)
.(C)
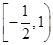 . (D).
. (D).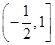
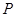 是单位圆和
是单位圆和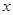 轴正半轴的交点,
轴正半轴的交点,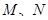 是单位圆上的两点,
是单位圆上的两点,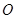 是坐
是坐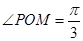 ,
,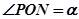 ,
,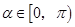 ,
,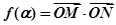 ,则
,则 的范围为 ( )
的范围为 ( )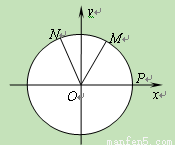
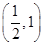 (B)
(B) 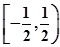 .(C)
.(C)
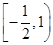 . (D).
. (D).