题目内容
过双曲线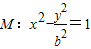 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是( )
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是( )A.

B.
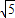
C.
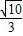
D.
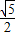
【答案】分析:过双曲线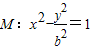 的左顶点A(1,0)作斜率为1的直线l:y=x-1,若l与双曲线M的两条渐近线
的左顶点A(1,0)作斜率为1的直线l:y=x-1,若l与双曲线M的两条渐近线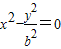 ,分别相交于点B(x1,y1),C(x2,y2),联立方程组代入消元得(b2-1)x2+2x-1=0,然后由根与系数的关系求出x1和x2的值,进而求出双曲线M的离心率.
,分别相交于点B(x1,y1),C(x2,y2),联立方程组代入消元得(b2-1)x2+2x-1=0,然后由根与系数的关系求出x1和x2的值,进而求出双曲线M的离心率.
解答:解:过双曲线 的右顶点A(1,0)作斜率为1的直线l:y=x-1,
的右顶点A(1,0)作斜率为1的直线l:y=x-1,
若l与双曲线M的两条渐近线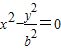 分别相交于点B(x1,y1),C(x2,y2),
分别相交于点B(x1,y1),C(x2,y2),
联立方程组代入消元得(b2-1)x2+2x-1=0,
∴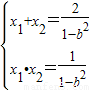 ,
,
∴x1+x2=2x1x2,
又|AB|=|BC|,则B为AC中点,2x1=1+x2,
代入解得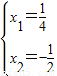 ,
,
∴b2=9,双曲线M的离心率e=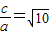 ,
,
故选A.
点评:本题考题双曲线性质的综合运用,解题过程中要注意根与系数的关系的运用.
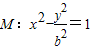 的左顶点A(1,0)作斜率为1的直线l:y=x-1,若l与双曲线M的两条渐近线
的左顶点A(1,0)作斜率为1的直线l:y=x-1,若l与双曲线M的两条渐近线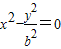 ,分别相交于点B(x1,y1),C(x2,y2),联立方程组代入消元得(b2-1)x2+2x-1=0,然后由根与系数的关系求出x1和x2的值,进而求出双曲线M的离心率.
,分别相交于点B(x1,y1),C(x2,y2),联立方程组代入消元得(b2-1)x2+2x-1=0,然后由根与系数的关系求出x1和x2的值,进而求出双曲线M的离心率.解答:解:过双曲线
 的右顶点A(1,0)作斜率为1的直线l:y=x-1,
的右顶点A(1,0)作斜率为1的直线l:y=x-1,若l与双曲线M的两条渐近线
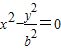 分别相交于点B(x1,y1),C(x2,y2),
分别相交于点B(x1,y1),C(x2,y2),联立方程组代入消元得(b2-1)x2+2x-1=0,
∴
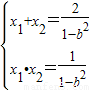 ,
,∴x1+x2=2x1x2,
又|AB|=|BC|,则B为AC中点,2x1=1+x2,
代入解得
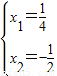 ,
,∴b2=9,双曲线M的离心率e=
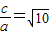 ,
,故选A.
点评:本题考题双曲线性质的综合运用,解题过程中要注意根与系数的关系的运用.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
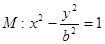 的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且
的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B.C,且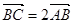 ,则双曲线M的离心率是( )
,则双曲线M的离心率是( )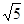 B.
B.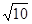 C.
C.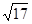 D.
D.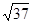
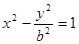 的左顶点A作斜率为1的直线l,若直线l与该双曲线的两条渐近线分别相交于点B、C,且|AB|=|BC|,则双曲线的离心率e=
。
的左顶点A作斜率为1的直线l,若直线l与该双曲线的两条渐近线分别相交于点B、C,且|AB|=|BC|,则双曲线的离心率e=
。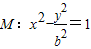 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是( )
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是( )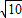
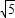

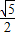
 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是 .
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是 .