题目内容
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. | B. | C. | D.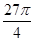 |
A.
解析试题分析:如图2,正四棱锥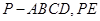 为其高,
为其高,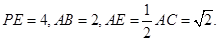 设球心为
设球心为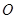 ,连结
,连结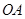 ,设球半径为
,设球半径为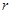 .在
.在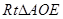 中,由勾股定理得
中,由勾股定理得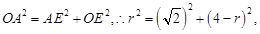 解得
解得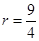 ,
,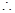 该球的表面积为
该球的表面积为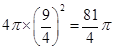 ,故选A.
,故选A.
考点:1.球的内接正四棱锥问题;2. 球的表面积的计算.

练习册系列答案
相关题目
如图(1)、(2)、(3)、(4)为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
| A.①和② | B.③和① | C.④和③ | D.④和② |
某几何体的三视图如图所示,则该几何体的体积为
| A.12 | B.18 | C.24 | D.30 |
已知某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
 ,4的对面的数字为
,4的对面的数字为 ,则
,则 ( )
( )






