题目内容
设AB、BC、CD是不在同一平面内的三条线段, 则过这三条线段中点的平面与AC的位置关系是_________.
答案：平行
解析：
解析：
|
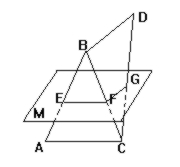
解: 如图, 设线段AB、BC、CD的中点分别是E、F、G, 过三点E、F、G的平面是M. 连结EF、FG, 则由△ABC得EF∥AC. 现在证明AC不在平面M内. 用反证法. 假定直线AC在平面M内, 那么点C和G都在平面M内, 因而通过这两点的直线CD在平面M内. 同理直线AB和BC也都在平面M内. 但已知AB、BC、CD不在同一平面内, 导致矛盾. 所以AC不在平面M内. 平面M外的直线AC平行于平面M内的直线EF, 所以AC∥平面M.
|
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设
AB、BC、CD是不在同一平面内的三条线段，则经过它们中点的平面和直线AC的位置关系是[
]|
A ．平行 |
B ．相交 |
|
C ．平行或相交 |
D ．AC在此平面内 |