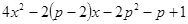题目内容
已知函数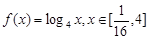 的值域为集合
的值域为集合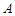 ,关于
,关于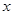 的不等式
的不等式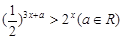 的解集为
的解集为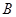 ,集合
,集合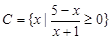 ,集合
,集合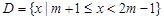
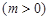
(1)若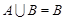 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若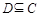 ,求实数
,求实数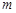 的取值范围。
的取值范围。
(1) ;(2)
;(2)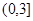 ,
,
解析试题分析:(1)本小题主要考查不等式的解法、以及集合的基本关系,根据函数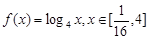 单调性可求集合
单调性可求集合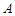 ;利用
;利用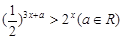 可求集合
可求集合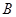 ;然后利用
;然后利用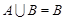 可分析实数
可分析实数 的取值范围;(2)先解集合
的取值范围;(2)先解集合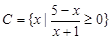 ,然后根据
,然后根据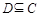 可分析实数
可分析实数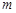 的取值范围
的取值范围
试题解析:(1)因为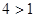 ,所以
,所以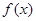 在
在 上,单调递增,
上,单调递增,
所以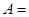
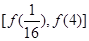
 , 2分
, 2分
又由 可得:
可得: 即:
即: ,所以
,所以 ,
,
所以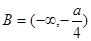 , 4分
, 4分
又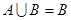 所以可得:
所以可得: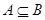 , 5分
, 5分
所以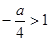 ,所以
,所以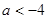 即实数
即实数 的取值范围为
的取值范围为 6分
6分
(2)因为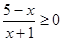 ,所以有
,所以有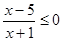 ,,所以
,,所以 , 8分
, 8分
对于集合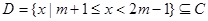 有:
有:
①当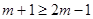 时,即
时,即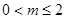 时
时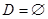 ,满足
,满足 10分
10分
②当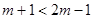 时,即
时,即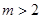 时
时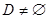 ,所以有:
,所以有:
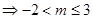 ,又因为
,又因为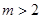 ,所以
,所以 13分
13分
综上:由①②可得:实数 的取值范围为
的取值范围为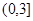 14分
14分
考点:不等式的解法,集合的基本关系

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
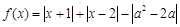 ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数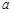 的取值范围.
的取值范围.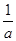 +
+ +
+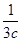 =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.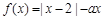 .
.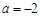 时,解不等式
时,解不等式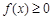 ;
;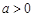 时,不等式
时,不等式 的解集为
的解集为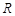 ,求实数
,求实数 的取值范围.
的取值范围.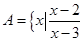 <
<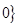 ,
,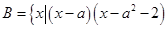 <
< 时,求
时,求 ;
;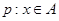 ,命题
,命题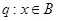 ,若q是p的必要条件,求实数
,若q是p的必要条件,求实数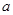 的取值范围.
的取值范围.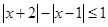 .
.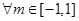 ,不等式a2-5a-3≥
,不等式a2-5a-3≥ 恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。
恒成立,若命题“P或Q”为真命题,且“P且Q”为假命题,求实数a的范围。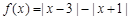 ,
,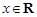 .
. ;
;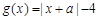 ,且
,且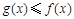 在
在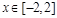 上恒成立,求实数
上恒成立,求实数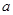 的取值范围.
的取值范围.