题目内容
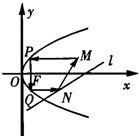 如图,从点M(x0,2)发出的光线沿平行于抛物线y2=4x的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线l:x-2y-7=0上的点N,再反射后又射回点M,则x0=
如图,从点M(x0,2)发出的光线沿平行于抛物线y2=4x的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线l:x-2y-7=0上的点N,再反射后又射回点M,则x0=分析:由题意可得抛物线的轴为x轴,抛物线的焦点F(1,0),MP所在的直线方程为y=2,从而可求P(1,2),Q(1,-2),N(3,-2),再根据直线的到角公式可求直线MN的斜率k,写出直线MN的方程,再令y=2可求答案.
解答:解:由题意可得抛物线的轴为x轴F(1,0),∴MP所在的直线方程为y=2
在抛物线方程y2=4x中令y=2可得x=1即P(1,2)
从而可得Q(1,-2),N(3,-2)
设MN所在的直线方程的斜率为k,则根据直线的到角公式可得
=
解方程可得,k=
即直线MN的方程为y+2=
(x-3)
令y=2可得x0=6
故答案为:6
在抛物线方程y2=4x中令y=2可得x=1即P(1,2)
从而可得Q(1,-2),N(3,-2)
设MN所在的直线方程的斜率为k,则根据直线的到角公式可得
k-
| ||
1+
|
| 1 |
| 2 |
解方程可得,k=
| 4 |
| 3 |
即直线MN的方程为y+2=
| 4 |
| 3 |
令y=2可得x0=6
故答案为:6
点评:本题主要考查了抛物线的性质的应用,直线方程的夹角(到角)公式的应用,直线方程的求解,解决问题的关键是要熟练掌握相关的性质并能灵活应用.

练习册系列答案
相关题目
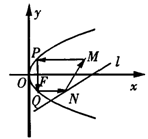 如图,从点
如图,从点