题目内容
设函数
，若f（4）=f（0），f（2）=2，则函数g（x）=f（x）-x的零点的个数是（ ）A．0
B．1
C．2
D．3
【答案】分析：根据分段函数的表达式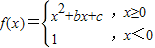
，因为f（4）=f（0），f（2）=2，代入求得b与c，可以代入函数g（x）=f（x）-x=0，可以求出零点，从而求解；
解答：解：∵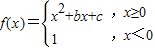
，
∴f（4）=f（0），f（2）=2，
即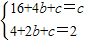
，
∴
，
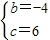若x≥0，则x2-4x+6=x，
∴x=2，或x=3；
若x＜0，则x=1舍去，
故选C．
点评：此题主要考查分段函数的性质及其应用，还考查函数零点问题，本题比较简单，是一道基础题；
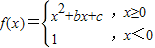，因为f（4）=f（0），f（2）=2，代入求得b与c，可以代入函数g（x）=f（x）-x=0，可以求出零点，从而求解；解答：解：∵
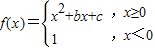，∴f（4）=f（0），f（2）=2，
即
，∴
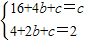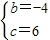，若x≥0，则x2-4x+6=x，
∴x=2，或x=3；
若x＜0，则x=1舍去，
故选C．
点评：此题主要考查分段函数的性质及其应用，还考查函数零点问题，本题比较简单，是一道基础题；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
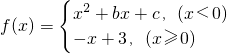，若f（-4）=f（0），f（-2）=-1，
，若f（-4）=f（0），f（-2）=-2，则函数g（x）=f（x）-x的零点个数为 ．
，若f（-4）=f（0），f（-2）=-1，
，若f（4）=f（0），f（2）=2，则函数g（x）=f（x）-x的零点的个数是（ ）