题目内容
如图，在矩形
中，
，以
为圆心1为半径的圆与
交于
（圆弧
为圆在矩形内的部分）
（1）在圆弧上确定
点的位置，使过的切线
平分矩形ABCD的面积；
（2）若动圆
与满足题（1）的切线及边
都相切，试确定的位置，使圆为矩形内部面积最大的圆．
解：
（1）以A点为坐标原点，AB所在直线为x轴，建立直角坐标系．
设
，
，
，圆弧
的方程
切线l的方程：
（可以推导：设直线
的斜率为
，由直线与圆弧相切知：
，所以
，从而有直线的方程为
，化简即得）．
设与
交于
可求F（
），G（
），
l平分矩形ABCD面积，
……①
又
……② 解①、②得：
．
（2）由题（Ⅰ）可知：切线l的方程：
，
当满足题意的圆
面积最大时必与边
相切，设圆与直线、
分别切于
，则
（
为圆的半径）．
，
由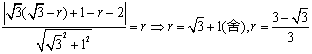
．
点坐标为
．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=2，AD=1，E是CD的中点，以AE为折痕将△DAE向上折起，使D为D′，且平面D′AE⊥平面ABCE．
如图，在矩形ABCD中，
如图，在矩形ABCD中，AB=2，AD=1，E是CD的中点，以AE为折痕将△DAE向上折起，使D为D′，且平面D′AE⊥平面ABCE．