题目内容
 已知有向线段
已知有向线段 的起点P(-1,1),终点Q(2,2),若直线l:x+my+m=0与有向线段
的起点P(-1,1),终点Q(2,2),若直线l:x+my+m=0与有向线段 的延长线相交,且过定点M(0,-1).如图,则m的取值范围是
的延长线相交,且过定点M(0,-1).如图,则m的取值范围是
- A.(
 ,
, )
) - B.(-3,-
 )
) - C.(-∞,-3)
- D.(-
 ,+∞)
,+∞)
B
分析:先求出PQ的斜率,再分情况讨论出直线的几种特殊情况,综合即可得到答案.
解答:由题知kPQ= =
= ,
,
直线x+my+m=0过点M(0,-1).
当m=0时,直线化为x=0,一定与PQ相交,所以m≠0,
当m≠0时,k1=- ,考虑直线l的两个极限位置.
,考虑直线l的两个极限位置.
(1)l经过Q,即直线l1,则kl1=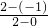 =
= ;
;
(2)l与 平行,即直线l2,则kl2=kPQ=
平行,即直线l2,则kl2=kPQ= ,
,
所以 <-
<- <
< ,
,
即-3<m<- .
.
故选B.
点评:本题主要是考查平面向量以及直线之间的位置关系的综合题.其中涉及到分类讨论思想的应用,属于基础题目.
分析:先求出PQ的斜率,再分情况讨论出直线的几种特殊情况,综合即可得到答案.
解答:由题知kPQ=
 =
= ,
,直线x+my+m=0过点M(0,-1).
当m=0时,直线化为x=0,一定与PQ相交,所以m≠0,
当m≠0时,k1=-
 ,考虑直线l的两个极限位置.
,考虑直线l的两个极限位置.(1)l经过Q,即直线l1,则kl1=
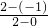 =
= ;
;(2)l与
 平行,即直线l2,则kl2=kPQ=
平行,即直线l2,则kl2=kPQ= ,
,所以
 <-
<- <
< ,
,即-3<m<-
 .
.故选B.
点评:本题主要是考查平面向量以及直线之间的位置关系的综合题.其中涉及到分类讨论思想的应用,属于基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知有向线段
已知有向线段 的起点P(-1,1),终点Q(2,2),若直线l:x+my+m=0与有向线段
的起点P(-1,1),终点Q(2,2),若直线l:x+my+m=0与有向线段 的延长线相交,且过定点M(0,-1).如图,则m的取值范围是( )
的延长线相交,且过定点M(0,-1).如图,则m的取值范围是( )
 ,
, )
) )
) ,+∞)
,+∞)