题目内容
(本小题满分13分)
已知数列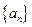 的前
的前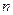 项和为
项和为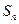 ,
,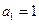 ,
,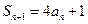 ,设
,设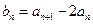 .
.
(Ⅰ)证明数列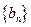 是等比数列;
是等比数列;
(Ⅱ)数列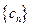 满足
满足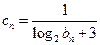
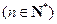 ,设
,设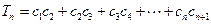 ,若对一切
,若对一切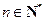 不等式
不等式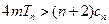 恒成立,求实数
恒成立,求实数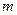 的取值范围.
的取值范围.
已知数列
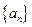 的前
的前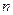 项和为
项和为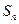 ,
,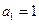 ,
,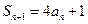 ,设
,设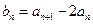 .
.(Ⅰ)证明数列
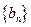 是等比数列;
是等比数列;(Ⅱ)数列
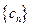 满足
满足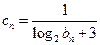
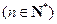 ,设
,设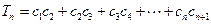 ,若对一切
,若对一切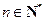 不等式
不等式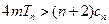 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(1)略(2)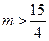
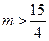
(Ⅰ)由于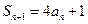 , ①
, ①
当 时,
时,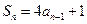 . ②
. ②
① ②得
②得 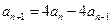 .
.
所以 .…………………………………………………2分
.…………………………………………………2分
又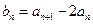 ,
,
所以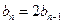 .
.
因为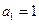 ,且
,且 ,
,
所以 .
.
所以 .
.
故数列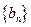 是首项为
是首项为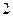 ,公比为
,公比为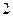 的等比数列.…………………………………6分
的等比数列.…………………………………6分
(Ⅱ)由(Ⅰ)可知 ,则
,则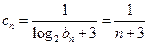 (
( ).
).
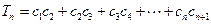
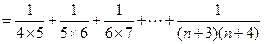
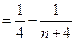
 .……………………………………………………………………9分
.……………………………………………………………………9分
由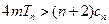 ,得
,得 .
.
即 .
.
所以 .
.
所以 .……………………………………11分
.……………………………………11分
设 ,
,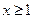 .
.
可知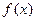 在
在 为减函数,又
为减函数,又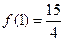 ,
,
则当 时,有
时,有 .
.
所以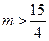 .
.
故当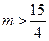 时,
时,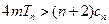 恒成立.…………………………………13分
恒成立.…………………………………13分
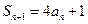 , ①
, ①当
 时,
时,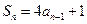 . ②
. ②①
 ②得
②得 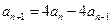 .
.所以
 .…………………………………………………2分
.…………………………………………………2分又
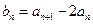 ,
,所以
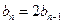 .
.因为
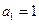 ,且
,且 ,
,所以
 .
.所以
 .
.故数列
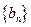 是首项为
是首项为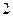 ,公比为
,公比为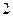 的等比数列.…………………………………6分
的等比数列.…………………………………6分(Ⅱ)由(Ⅰ)可知
 ,则
,则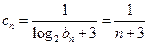 (
( ).
).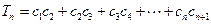
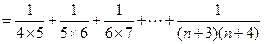
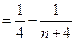
 .……………………………………………………………………9分
.……………………………………………………………………9分由
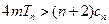 ,得
,得 .
.即
 .
.所以
 .
.所以
 .……………………………………11分
.……………………………………11分设
 ,
,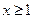 .
.可知
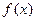 在
在 为减函数,又
为减函数,又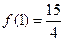 ,
,则当
 时,有
时,有 .
.所以
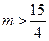 .
.故当
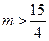 时,
时,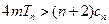 恒成立.…………………………………13分
恒成立.…………………………………13分
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
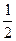
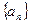 中,
中,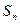 是前
是前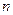 项和,且
项和,且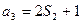 ,
,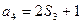 ,则
,则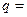 * * * .
* * * .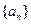 的前
的前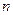 项和为
项和为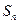 ,则
,则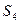 ,
,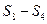 ,
,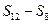 ,
,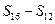 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列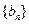 的前
的前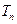 ,则
,则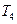 , , ,
, , ,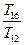 成等比数列.
成等比数列.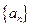 的前
的前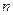 项和
项和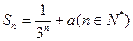 ,且
,且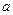 是常数,则此无穷等比数列各项的和等于 (用数值作答).
是常数,则此无穷等比数列各项的和等于 (用数值作答).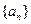 是等比数列,且
是等比数列,且 ,
, ,则
,则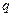 为
为