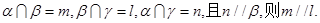题目内容
设l、m、n表示不同的直线,α、β、γ表示不同的平面,给出下列4个命题:①若m∥l,且m⊥α,则l⊥α;
②若m∥l,且m∥α,则l∥α;
③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;
④若α∩β=m,β∩γ=l,α∩γ=n,且n∥β,则m∥l.
其中正确命题的个数是( )
A.1
B.2
C.3
D.4
【答案】分析:本题考查的是直线之间,直线与平面之间的位置关系,可借助图象解答.
解答:解:易知命题①正确;在命题②的条件下,直线l可能在平面α内,故命题为假;在命题③的条件下,三条直线可以相交于一点,故命题为假;在命题④中,由α∩γ=n知,n?α且n?γ,由n?α及∥βα∩β=m,得n∥m,同理n∥l,故m∥l,命题④正确.
故答案选B.
点评:本题主要考查了直线与直线间的位置关系,以及直线与平面间的位置关系,注意二者的联系与区别.
解答:解:易知命题①正确;在命题②的条件下,直线l可能在平面α内,故命题为假;在命题③的条件下,三条直线可以相交于一点,故命题为假;在命题④中,由α∩γ=n知,n?α且n?γ,由n?α及∥βα∩β=m,得n∥m,同理n∥l,故m∥l,命题④正确.
故答案选B.
点评:本题主要考查了直线与直线间的位置关系,以及直线与平面间的位置关系,注意二者的联系与区别.

练习册系列答案
相关题目
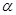 、
、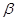 、
、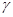 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题: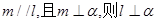 ;
;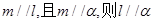 ;
;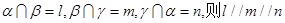 ;
;