题目内容
△ABC内接于以O为圆心的圆,且 .则∠C=________°,cosA=________.
.则∠C=________°,cosA=________.
135 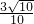
分析:将所给的等式中的5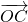 移到等式的一边,将等式平方求出
移到等式的一边,将等式平方求出 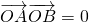 ,可求出∠AOB,即
,可求出∠AOB,即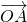 与
与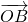 的夹角,再通过圆心角与圆周角的关系,求得∠C,而∠A是∠BOC的一半,可用半角公式进行计算.
的夹角,再通过圆心角与圆周角的关系,求得∠C,而∠A是∠BOC的一半,可用半角公式进行计算.
解答:∵
∴
∴ =
=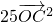
∵A,B,C在圆上
设OA=OB=OC=1
∴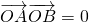
根据 得出A,B,C三点在圆心的同一侧
得出A,B,C三点在圆心的同一侧
∴根据圆周角定理知∠C=180°-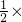 90°=135°
90°=135°
同理求出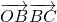 =
= ,
,
cos∠BOC=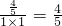
∵∠A是∠BOC的一半
∴
故答案为:135°;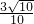
点评:本题考查向量的运算和三角形外心的性质和应用,本题解题的关键是对于所给的向量式的整理,注意向量运算法则的灵活运用.
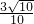
分析:将所给的等式中的5
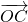 移到等式的一边,将等式平方求出
移到等式的一边,将等式平方求出 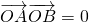 ,可求出∠AOB,即
,可求出∠AOB,即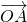 与
与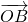 的夹角,再通过圆心角与圆周角的关系,求得∠C,而∠A是∠BOC的一半,可用半角公式进行计算.
的夹角,再通过圆心角与圆周角的关系,求得∠C,而∠A是∠BOC的一半,可用半角公式进行计算.解答:∵

∴

∴
 =
=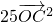
∵A,B,C在圆上
设OA=OB=OC=1
∴
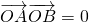
根据
 得出A,B,C三点在圆心的同一侧
得出A,B,C三点在圆心的同一侧∴根据圆周角定理知∠C=180°-
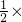 90°=135°
90°=135°同理求出
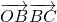 =
= ,
,cos∠BOC=
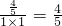
∵∠A是∠BOC的一半
∴

故答案为:135°;
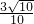
点评:本题考查向量的运算和三角形外心的性质和应用,本题解题的关键是对于所给的向量式的整理,注意向量运算法则的灵活运用.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
△ABC内接于以O为圆心,1为半径的圆,且3
+4
+5
=
,则
•
的值为( )
| OA |
| OB |
| OC |
| 0 |
| OC |
| AB |
A、-
| ||
B、
| ||
C、-
| ||
D、
|