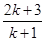题目内容
用数学归纳法证明“
<n+1 (n∈N*)”.第二步证n=k+1时(n=1已验证,n=k已假设成立),这样证明:
=
<
=(k+1)+1,所以当n=k+1时,命题正确.此种证法( )
| n2+n |
| (k+1)2+(k+1) |
| k2+3k+2 |
| k2+4k+4 |
分析:必须利用归纳假设才是数学归纳法.
解答:解:应该这样证明:假设当n=k≥2时,
<k+1成立,
则当n=k+1时,左边=
=
<
=(k+1)+1,∴n=k+1时,不等式也成立.
而原证法只是应用了放缩法和不等式的性质,没有应用归纳假设,故不符合数学归纳法的要求.
故选D.
| k2+k |
则当n=k+1时,左边=
| (k+1)2+k+1 |
| k2+k+2k+2 |
| (k+1)2+1+2k+2 |
而原证法只是应用了放缩法和不等式的性质,没有应用归纳假设,故不符合数学归纳法的要求.
故选D.
点评:正确理解数学归纳法证明命题的要求是解题的关键.

练习册系列答案
相关题目
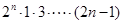 (n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
(n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )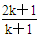 D.
D.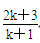
 D..
D..