题目内容
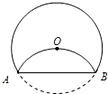 如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为
如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为2
| 3 |
2
cm.| 3 |
分析:取AB的中点M,连结OA、OM.根据题意,可得Rt△AOM中AO=2cm,OM=1cm,利用勾股定理算出AM=
cm,可得折痕AB的长.
| 3 |
解答:解: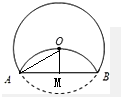 取AB的中点M,连结OA、OM,
取AB的中点M,连结OA、OM,
∵M为AB的中点,∴OM⊥AB
∵纸片折叠后,圆弧恰好经过圆心O,
∴设半径为R,OM=
R=1cm.
Rt△AOM中,AM=
=
cm,可得AB=2AM=2
cm.
故答案为:2
 取AB的中点M,连结OA、OM,
取AB的中点M,连结OA、OM,∵M为AB的中点,∴OM⊥AB
∵纸片折叠后,圆弧恰好经过圆心O,
∴设半径为R,OM=
| 1 |
| 2 |
Rt△AOM中,AM=
| AO2-OM2 |
| 3 |
| 3 |
故答案为:2
| 3 |
点评:本题给出实际问题,求折痕AB的长.着重考查了垂径定理和圆中的弦长求法等知识,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目