题目内容
已知圆C的圆心在射线3x-y=0(x≥0)上,圆C与x轴相切,且被直线x-y=0截得的弦长为2
.
(1)求圆C的方程;
(2)点为圆C上任意一点,不等式x+y+m≥0恒成立,求实数m的取值范围.
| 7 |
(1)求圆C的方程;
(2)点为圆C上任意一点,不等式x+y+m≥0恒成立,求实数m的取值范围.
分析:(1)依题意设圆心坐标为(a,3a)(a>0),由圆与x轴相切,得到半径为|3a|,进而表示出圆C的标准方程,由垂径定理及勾股定理表示出圆心到直线y=x的距离d,再利用点到直线的距离公式表示出圆心到直线y=x的距离,两者相等列出关于a的方程,求出方程的解得到a的值,即可确定出圆C的方程;
(2)由(1)求出的圆C方程,设x=1+3cosθ,y=3+3sinθ(θ∈[0,2π]),代入已知的不等式中,分离出m,去括号整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由不等式恒成立得到m大于等于-x-y的最大值,由正弦函数的值域确定出-x-y的最大值,即可得到满足题意m的范围.
(2)由(1)求出的圆C方程,设x=1+3cosθ,y=3+3sinθ(θ∈[0,2π]),代入已知的不等式中,分离出m,去括号整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由不等式恒成立得到m大于等于-x-y的最大值,由正弦函数的值域确定出-x-y的最大值,即可得到满足题意m的范围.
解答:解:(1)依题设圆心坐标(a,3a)(a>0),
∵圆与x轴相切,∴圆的半径R=|3a|,
∴圆C的方程可设为(x-a)2+(y-3a)2=9a2,
∵R=|3a|,弦长为2
,
∴圆心到直线y=x的距离d=
=
,
由点到直线的距离公式得:d=
,
∴
=
,
解得:a=±1,
又a>0,∴a=1,
则圆C方程为(x-1)2+(y-3)2=9;
(2)设x=1+3cosθ,y=3+3sinθ(θ∈[0,2π]),
则m≥-x-y=-(1+3cosθ)-(3+3sinθ)=-4-3sinθ-3cosθ=-4-3
sin(θ+
),
∵对任意θ∈[0,2π]恒成立,∴m≥(-x-y)max,
∵(-x-y)max=-4+3
,
∴m≥-4+3
.
∵圆与x轴相切,∴圆的半径R=|3a|,
∴圆C的方程可设为(x-a)2+(y-3a)2=9a2,
∵R=|3a|,弦长为2
| 7 |
∴圆心到直线y=x的距离d=
(3a)2-(
|
| 9a2-7 |
由点到直线的距离公式得:d=
| |a-3a| | ||
|
∴
| 9a2-7 |
| |a-3a| | ||
|
解得:a=±1,
又a>0,∴a=1,
则圆C方程为(x-1)2+(y-3)2=9;
(2)设x=1+3cosθ,y=3+3sinθ(θ∈[0,2π]),
则m≥-x-y=-(1+3cosθ)-(3+3sinθ)=-4-3sinθ-3cosθ=-4-3
| 2 |
| π |
| 4 |
∵对任意θ∈[0,2π]恒成立,∴m≥(-x-y)max,
∵(-x-y)max=-4+3
| 2 |
∴m≥-4+3
| 2 |
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,垂径定理,勾股定理,点到直线的距离公式,圆的极坐标方程,不等式恒成立问题,以及正弦函数的定义域与值域,是一道综合性较强的题.

练习册系列答案
相关题目
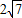 .
. ,则圆C的方程是( )
,则圆C的方程是( )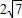 .
.