题目内容
已知在等比数列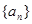 中,
中,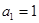 ,且
,且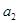 是
是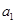 和
和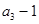 的等差中项.
的等差中项.
(Ⅰ)求数列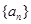 的通项公式;
的通项公式;
(Ⅱ)若数列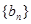 满足
满足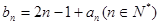 ,求
,求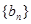 的前
的前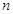 项和
项和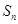 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)设公比是 ,依据等比数列的通项公式表示出
,依据等比数列的通项公式表示出 和
和 ,再由已知条件“
,再由已知条件“ 是
是 和
和 的等差中项”,结合等差中项的性质得到
的等差中项”,结合等差中项的性质得到 ,解出
,解出 ,代入等比数列的通项公式;(Ⅱ)先由(Ⅰ)中解得的
,代入等比数列的通项公式;(Ⅱ)先由(Ⅰ)中解得的 ,求出数列
,求出数列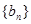 的通项公式:
的通项公式: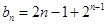 ,观察可知它可以分为一个等差数列
,观察可知它可以分为一个等差数列 和一个等比数列
和一个等比数列 ,结合等差数列和等比数列的前
,结合等差数列和等比数列的前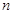 项和公式求
项和公式求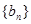 的前
的前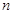 项和
项和 .
.
试题解析:(Ⅰ)设公比为 ,
,
则 ,
, ,
,
∵ 是
是 和
和 的等差中项,
的等差中项,
∴ ,
,
即
解得 ,
,
∴ .
.
(Ⅱ)由(Ⅰ)可知, ,
,
则

 .
.
考点:1.等差数列的前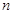 项和;2.等比数列的前
项和;2.等比数列的前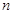 项和;3.等差中项;4.等比数列的通项公式
项和;3.等差中项;4.等比数列的通项公式

练习册系列答案
相关题目
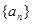 中,
中,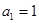 ,且
,且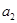 是
是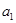 和
和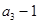 的等差中项.
的等差中项.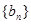 满足
满足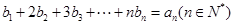 ,求
,求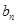 .
.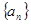 中,各项均为正数,且
中,各项均为正数,且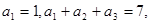 则数列
则数列