题目内容
某四面体的三视图如图所示.该四面体的六条棱的长度中,最大的是( )
A. | B. |
C. | D. |
C
解析试题分析:由三视图可知原几何体为三棱锥,其中底面△ABC为俯视图中的钝角三角形,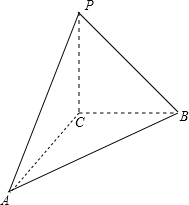
∠BCA为钝角,其中BC=2,BC边上的高为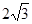 ,PC⊥底面ABC,且PC=2,由以上条件可知,∠PCA为直角,最长的棱为PA或AB,在直角三角形PAC中,由勾股定理得,PA=
,PC⊥底面ABC,且PC=2,由以上条件可知,∠PCA为直角,最长的棱为PA或AB,在直角三角形PAC中,由勾股定理得,PA=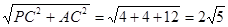 ,
,
在钝角三角形ABC中,AB=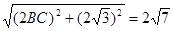 .故选C.
.故选C.
考点:1.棱锥的结构特征;2.点、线、面间的距离计算

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
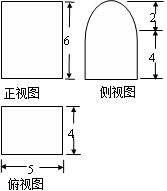
已知某几何体的三视图如图所示,则该几何体的表面积等于( )
A.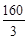 | B.160 | C. | D.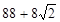 |
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A.2πR2 | B. πR2 πR2 |
C.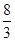 πR2 πR2 | D. πR2 πR2 |
一个几何体的三视图如图所示,已知这个几何体的体积为 ,则h的值为( )
,则h的值为( )
A. | B. | C. | D.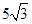 |
一个几何体的三视图如图所示,则该几何体的体积是( )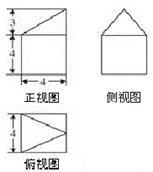
| A.64 | B.72 | C.80 | D.112 |
一个直三棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
| A.9 | B.10 | C.11 | D. |









 上、下底面中心分别为
上、下底面中心分别为 ,将正方体绕直线
,将正方体绕直线 旋转一周,其中由线段
旋转一周,其中由线段 旋转所得图形是( )
旋转所得图形是( )