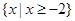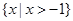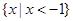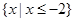题目内容
已知A={x||x-a|<4},B={x|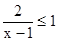 }.
}.
(1)若a=1,求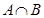 ;
;
(2)若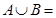 R,求实数a的取值范围.
R,求实数a的取值范围.
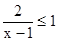 }.
}. (1)若a=1,求
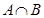 ;
; (2)若
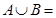 R,求实数a的取值范围.
R,求实数a的取值范围.解:(1) a=1时,A=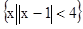 =
=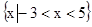
B=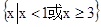
∴A∩B=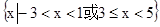 ---------6分
---------6分
(2)∵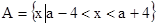 B=
B=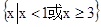
且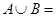 R
R
∴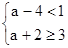 解得:
解得: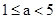
∴实数a的取值范围是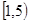 -------------12分
-------------12分
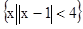 =
=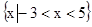
B=
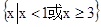
∴A∩B=
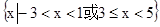 ---------6分
---------6分(2)∵
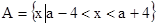 B=
B=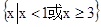
且
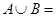 R
R∴
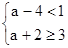 解得:
解得: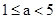
∴实数a的取值范围是
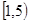 -------------12分
-------------12分本试题主要是考查了集合的交集和并集的运算的综合运用。
(1)因为a=1时,A=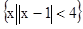 =
=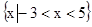
B=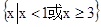
因此可知A∩B=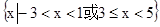 -
-
(2)∵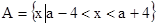 B=
B=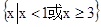
且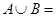 R
R
∴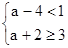 解得:
解得: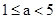
得到结论。
(1)因为a=1时,A=
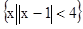 =
=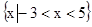
B=
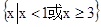
因此可知A∩B=
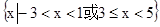 -
-(2)∵
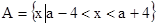 B=
B=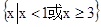
且
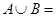 R
R∴
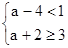 解得:
解得: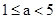
得到结论。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 UA)∪B为( )
UA)∪B为( ) 是p的必要条件,求实数a.
是p的必要条件,求实数a.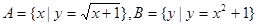 ,则
,则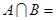 _____________.
_____________.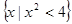 ,N=
,N=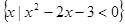 ,则集合M
,则集合M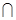 N=( )
N=( )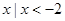 }
} }
} 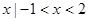 }
}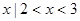 }
} ,则
,则 ( )
( ) ;
;  ;
;  ;
; ;
;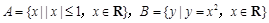 ,则
,则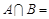 ( )
( )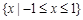
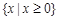
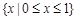
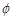
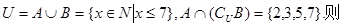 元素4属于哪一个集合判断正确的是( )
元素4属于哪一个集合判断正确的是( )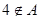
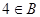
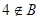
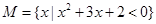 ,集合
,集合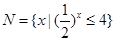 ,则
,则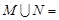 ( )
( )