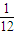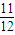题目内容
从甲、乙、丙、丁四个人中选两名代表,
求:(Ⅰ)甲被选中的概率;
(Ⅱ)丁没被选中的概率.
求:(Ⅰ)甲被选中的概率;
(Ⅱ)丁没被选中的概率.
分析:(Ⅰ)用列举法列举从4人中任取2人的情况,可得其情况数目,从中查找可得甲被选中的情况数目,由古典概型公式,计算可得答案;
(Ⅱ)有(Ⅰ)的情况,从中查找可得丁没有被选中的情况数目,进而由古典概型公式,计算可得答案.
(Ⅱ)有(Ⅰ)的情况,从中查找可得丁没有被选中的情况数目,进而由古典概型公式,计算可得答案.
解答:解:(Ⅰ)从甲、乙、丙、丁四个人中选两名代表,
共有(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁)6种情况,
其中甲被选中包含其中的三种情况.
所以甲被选中的概率为
=
.
(Ⅱ)由(1)可得,丁没有被选中的情况也有3种,
则丁没被选中的概率为
=
.
共有(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁)6种情况,
其中甲被选中包含其中的三种情况.
所以甲被选中的概率为
| 3 |
| 6 |
| 1 |
| 2 |
(Ⅱ)由(1)可得,丁没有被选中的情况也有3种,
则丁没被选中的概率为
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查列举法求古典概型的概率,注意列举时做到不重不漏即可.

练习册系列答案
相关题目