题目内容
如图，α，β分别为终边落在OM、ON位置上的两个角，且α=30°，β=300°终边落在阴影部分（含边界）时所有角的集合（以弧度制表示）为
{x|-
+2kπ≤x≤
+2kπ}（k∈Z）
| π |
| 3 |
| π |
| 6 |
{x|-
+2kπ≤x≤
+2kπ}（k∈Z）
．| π |
| 3 |
| π |
| 6 |
分析：根据题意，找出在[-π，π]范围内与α、β终边相同的角，再根据任意角的概念和终边相同角的集合表示法，可写出终边落在阴影部分（含边界）时所有角的集合．
解答：解：∵α=30°，β=300°
∴在[-π，π]范围内，与α、β终边相同的角分别为
、-
由终边相同角的集合表示，可得终边落在阴影部分（含边界）时所有角的
集合为{x|-
+2kπ≤x≤
+2kπ}（k∈Z）．
故答案为：{x|-
+2kπ≤x≤
+2kπ}（k∈Z）
解：∵α=30°，β=300°∴在[-π，π]范围内，与α、β终边相同的角分别为
| π |
| 6 |
| π |
| 3 |
由终边相同角的集合表示，可得终边落在阴影部分（含边界）时所有角的
集合为{x|-
| π |
| 3 |
| π |
| 6 |
故答案为：{x|-
| π |
| 3 |
| π |
| 6 |
点评：本题给出坐标系内的阴影部分区域，求终边落在阴影部分的角的集合．着重考查了弧度制和终边相同角的集合等知识，属于基础题．
练习册系列答案
相关题目
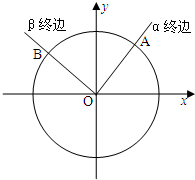
如图，以Ox为始边作任意角α，β，它们的终边与单位圆分别交于A，B点，则
•
的值等于（ ）
| OA |
| OB |
| A、sin（α+β） |
| B、sin（α-β） |
| C、cos（α+β） |
| D、cos（α-β） |
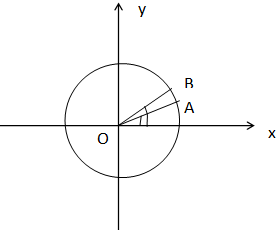如图，在平面直角坐标系xOy中，以Ox轴为始边做两个锐角α，β，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为
如图，角θ的始边OA落在ox轴上，其始边、终边与单位圆分别交于点A，C，θ∈（0，