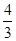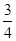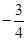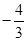题目内容
在直角坐标系xOy中.直线l过抛物线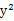 =4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。若直线l的倾斜角为60º.则△OAF的面积为
=4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。若直线l的倾斜角为60º.则△OAF的面积为
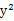 =4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。若直线l的倾斜角为60º.则△OAF的面积为
=4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。若直线l的倾斜角为60º.则△OAF的面积为 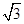
由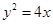 可求得焦点坐标
可求得焦点坐标 ,因为倾角60º,所以直线的斜率为
,因为倾角60º,所以直线的斜率为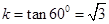 ,利用点斜式,直线方程为
,利用点斜式,直线方程为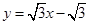 ,将直线和曲线联立
,将直线和曲线联立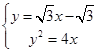
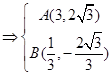 ,因此
,因此 .
.
【考点定位】本题考查的是解析几何中抛物线的问题,根据交点弦问题求围成面积。此题把握住抛物线的基本概念,熟练的观察出标准方程中的焦点和准线坐标和方程是成功的关键,当然还要知道三角形面积公式。
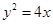 可求得焦点坐标
可求得焦点坐标 ,因为倾角60º,所以直线的斜率为
,因为倾角60º,所以直线的斜率为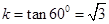 ,利用点斜式,直线方程为
,利用点斜式,直线方程为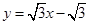 ,将直线和曲线联立
,将直线和曲线联立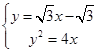
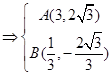 ,因此
,因此 .
.【考点定位】本题考查的是解析几何中抛物线的问题,根据交点弦问题求围成面积。此题把握住抛物线的基本概念,熟练的观察出标准方程中的焦点和准线坐标和方程是成功的关键,当然还要知道三角形面积公式。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
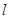
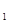 :
: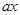 +
+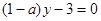 与直线
与直线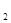 :
: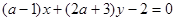 互相垂直,则
互相垂直,则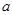 的值为( )
的值为( )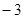
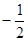
 或
或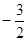
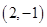 ,且与直线
,且与直线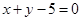 垂直的直线方程是 .
垂直的直线方程是 .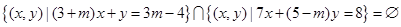 ,那
,那 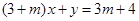 与两坐标轴所围成的三角形面积是_____ ___.
与两坐标轴所围成的三角形面积是_____ ___.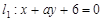 与
与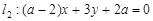 平行,则
平行,则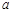 的值等于 ___.
的值等于 ___.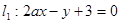 ,
,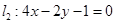 和
和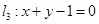 ,
,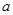 的取值范围;
的取值范围;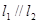 ,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到
,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到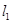 的距离是P点到
的距离是P点到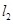 的距离的
的距离的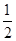 ;③P点到
;③P点到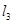 的距离之比是
的距离之比是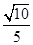 。若能,试求P点坐标;若不能,请说明理由。
。若能,试求P点坐标;若不能,请说明理由。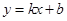 与曲线
与曲线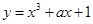 相切于点
相切于点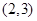 ,则
,则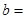 。
。 的斜率为( )
的斜率为( )