题目内容
一个暗箱里放着6个黑球、4个白球.(1)依次取出3个球,不放回,若第1次取出的是白球,求第3次取到黑球的概率;
(2)有放回地依次取出3个球,若第1次取出的是白球,求第3次取到黑球的概率;
(3)有放回地依次取出3个球,求取到白球个数ξ的分布列和期望.
分析:(1)第一次摸到白球的事件数为:C41×A92,在这条件下,第3次取到黑球分为两种情况:白黑黑,白白黑;故事件数为:C41•(C61C51+C31C61),即可计算
(2)因为每次取出之前暗箱的情况没有变化,所以每次取球互不影响,故第三次和第一次一样,概率为:
(3)有放回地依次取出3个球,相当于独立重复事件,即ξ~B(3,
),则可根据独立重复事件的定义知:P(ξ=k)=C3k(
)k(
)3-k,Eξ=3×
=
(2)因为每次取出之前暗箱的情况没有变化,所以每次取球互不影响,故第三次和第一次一样,概率为:
| 6 |
| 10 |
(3)有放回地依次取出3个球,相当于独立重复事件,即ξ~B(3,
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
解答:解:设事件A为“第1次取出的是白球,第3次取到黑球”,B为“第2次取到白球”,C为“第3次取到白球”,
则(1)P(A)=
=
.
(2)因为每次取出之前暗箱的情况没有变化,
所以每次取球互不影响,
所以P(
)=
=
.
(3)设事件D为“取一次球,取到白球”,
则P(D)=
,P(
)=
,
这3次取出球互不影响,
则ξ~B(3,
),
∴P(ξ=k)=
(
)k(
)3-k,(k=0,1,2,3).
Eξ=3×
=
则(1)P(A)=
| ||||||||||
|
| 2 |
| 3 |
(2)因为每次取出之前暗箱的情况没有变化,
所以每次取球互不影响,
所以P(
. |
| C |
| 6 |
| 10 |
| 3 |
| 5 |
(3)设事件D为“取一次球,取到白球”,
则P(D)=
| 2 |
| 5 |
. |
| D |
| 3 |
| 5 |
这3次取出球互不影响,
则ξ~B(3,
| 2 |
| 5 |
∴P(ξ=k)=
| C | k 3 |
| 2 |
| 5 |
| 3 |
| 5 |
Eξ=3×
| 2 |
| 5 |
| 6 |
| 5 |
点评:本小题主要考查条件概率.二项分布等知识,考查或然与必然的数学思想方法,以及数据处理能力.运算求解能力和应用意识.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
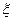 的分布列和期望.
的分布列和期望.