题目内容
已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2，则四面体ABCD的体积的最大值为
A． | B． | C． | D． |
B
解析
练习册系列答案
相关题目
[
B
D
的球
的直径
垂直于平面
，垂足为
，
是平面
、
分别
（B）
（D）
如图
是一平面图形的直观图，斜边
，则这个平面图形的面积是（ ）
A． | B．1 | C． | D． |
一个正三棱柱的主（正）视图是边长为
的正方形，则它的外接球的表面积等于（ ）
A． | B．  |
C．9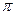 | D． |
题目内容
已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2，则四面体ABCD的体积的最大值为
| A． | B． | C． | D． |
B
解析
如图是一平面图形的直观图，斜边，则这个平面图形的面积是（ ）
| A． | B．1 | C． | D． |
一个正三棱柱的主（正）视图是边长为的正方形，则它的外接球的表面积等于（ ）
| A． | B． |
| C．9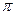 | D． |