Question

若x∈（2，4），a=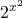，b=（2^x）²，c=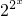，则a、b、c的大小关系是________．

Answer 1

a＞c＞b
分析：要比较a、b、c的大小关系，可以把a、b、c化简成以2为底的指数形式，主要是比较x²、2x、2^x的大小，然后借助于指数函数单调性得结论．
解答：b=（2^x）²=2^2x，a、b、c都是以2为底的指数形式，y=2^t在R上是增函数，只需要比较它们的指数x²、2x、2^x的大小就可以，
作差法：
（1）比较b、c大小时
构造f（x）=2^x-2x，则f^′（x）=2^xln2-2，f^′（x）为增函数，在x∈（2，4）上，最小值为4ln2-2，ln2≈0.6931，最小值大于0，故f^′（x）＞0．因此f（x）在（2，4）为增函数
又f（2）=0，所以当x∈（2，4）时，f（x）＞0，则2^x＞2x
∴c＞b
（2）比较a、c大小时
构造g（x）=x²-2^x，则g（x）在（0，+∞）上有两个交点（2，4），（4，16）且在x∈（2，4）上有x²＞2^x，
∴a＞c
综上，a、b、c的大小关系是a＞c＞b
故答案为a＞c＞b
点评：本题考查了不等式的大小比较，解答的关键是比较x²、2x、2^x的大小，其中运用了构造法，训练了函数的零点问题，同时考查了指数函数的单调性．