题目内容
设等差数列 的前n项和为Sn,若a1=-15, a3+a5= -18,则当Sn取最小值时n等于( )
的前n项和为Sn,若a1=-15, a3+a5= -18,则当Sn取最小值时n等于( )
| A.9 | B.8 | C.7 | D.6 |
B
解析试题分析:根据等差数列的性质化简a3+a5=-18,得到a4的值,然后根据a1的值,利用等差数列的通项公式即可求出公差d的值,根据a1和d的值写出等差数列的通项公式,进而写出等差数列的前n项和公式Sn,配方后即可得到Sn取最小值时n的值.解:由等差数列的性质可得 a3+a5=2a4=-18,解得a4=-9. 又a1=-15,设公差为d,所以,a4=a1+3d=-15+3d=-9,解得d="2" .则an=-15+2(n-1)=2n-17,那么可知所以a8<0, a9>0,当n=8时,Sn取最小值.故选B.
考点:等差数列的通项公式及前n项和公式
点评:此题考查学生灵活运用等差数列的通项公式及前n项和公式化简求值,掌握等差数列的性质,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在数列 等于( )
等于( )
A.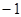 | B.1 | C.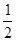 | D.2 |
在等差数列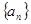 中,已知
中,已知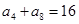 ,则
,则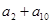 为 ( )
为 ( )
A.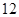 | B.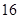 | C.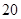 | D.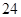 |
若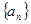 为等差数列,
为等差数列,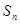 是其前n项的和,且
是其前n项的和,且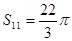 ,则
,则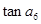 =( )
=( )
A.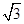 | B.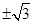 | C.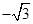 | D.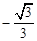 |
已知等差数列 中,
中, ,则
,则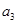 =( )
=( )
| A.10 | B.20 | C.30 | D.40 |
若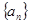 为等差数列,
为等差数列,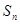 是其前
是其前 项的和,且
项的和,且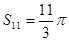 ,则
,则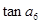 =( )
=( )
A.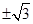 | B. | C.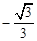 | D.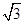 |
已知等差数列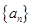 的公差和等比数列
的公差和等比数列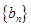 的公比都是
的公比都是 ,且
,且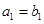 ,
,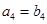 ,
,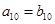 ,则
,则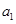 和
和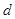 的值分别为( )
的值分别为( )
A.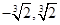 | B.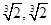 |
C.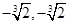 | D.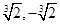 |
等差数列 ,
,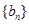 的前
的前 项和分别为
项和分别为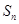 ,
, ,若
,若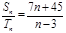 ,则使
,则使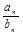 为整数的正整数n的取值个数是( )
为整数的正整数n的取值个数是( )
| A. 3 | B. 4 | C. 5 | D. 6 |
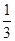 ,则D(3ξ-1)=( )
,则D(3ξ-1)=( )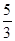 C、
C、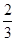 D、5
D、5