题目内容
.如图：正三棱柱ABC—A1B1C1中，D是BC的中点，AA1=AB=1．
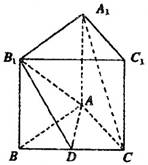
（1）求证：A1C//平面AB1D；
（2）求二面角B—AB1—D的大小；
（3）求点C到平面AB1D的距离．
【答案】
．过O作OH⊥面ABV，连结VH，
面VAB⊥面ABCD，OH⊥AB，OH⊥面ABV，∴OVH就是VO与VAB所成的角，
∴tan﹤VOH=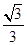
,∴﹤VOH=300
(2)过B作BM⊥VA，连接MC，∴﹤CMB为B-VA-C的平面角，
∴ tan﹤CMB =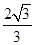
,∴﹤CMB=arctan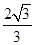
(3)VV—ABCD=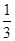 
SABCDH= 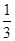a2 
a= 
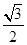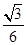a3
【解析】略
练习册系列答案
天天练口算系列答案
相关题目
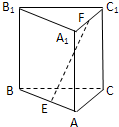如图，正三棱柱ABC-A1B1C1的各棱长（包括底面边长）都是2，E，F分别是AB，A1C1的中点，则EF与侧棱C1C所成的角的余弦值是（ ）
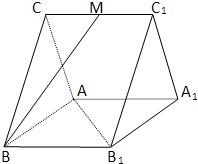如图，正三棱柱ABC-A1B1C1中，已知AB=AA1，M为CC1的中点．
如图，正三棱柱ABC-A1B1C1中，E是AC中点．
（2003•北京）如图，正三棱柱ABC-A1B1C1中，D是BC的中点，AB=a．