题目内容
在△ABC中,角A、B、C的对边分别是a、b.c,且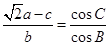 ,则B的大小为 .
,则B的大小为 .
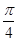
解析试题分析:因为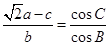 ,即(
,即(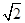 a-c)cosB=bcosC,由正弦定理得:(
a-c)cosB=bcosC,由正弦定理得:(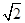 sinA-sinC)cosB=sinBcosC.∴
sinA-sinC)cosB=sinBcosC.∴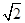 sinA•cosB-sinC•cosB=sinBcosC
sinA•cosB-sinC•cosB=sinBcosC
化为: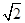 sinA•cosB=sinC•cosB+sinBcosC
sinA•cosB=sinC•cosB+sinBcosC
所以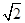 sinA•cosB=sin(B+C)
sinA•cosB=sin(B+C)
∵在△ABC中,sin(B+C)=sinA
∴2sinA•cosB=sinA,得:cosB=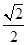 ,∴B=
,∴B=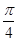 ,故答案为
,故答案为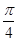 。
。
考点:本题主要考查正弦定理、余弦定理的应用,两角和的三角函数,三角函数诱导公式。
点评:中档题,研究三角形问题,一般有两种思路,即从边着手,主要利用余弦定理;二是从角入手,主要运用正弦定理。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
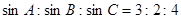 ,则cosC= .
,则cosC= .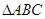 中,若
中,若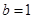 ,
,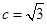 ,
,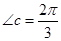 ,则
,则 = .
= .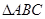 中,
中,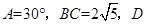 是
是 边上的一点,
边上的一点,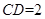 ,
, 的面积是4,则AC长为 .
的面积是4,则AC长为 . +b
+b ,
, ,其面积为
,其面积为 ,则
,则 。
。 中,角
中,角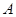 、
、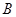 、
、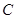 的对边分别为
的对边分别为 、
、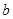 、
、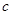 ,已知
,已知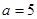 ,
,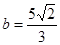 ,
,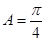 ,则
,则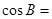 。
。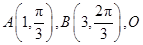 是极点,则
是极点,则 的面积等于_______;
的面积等于_______; 的不等式
的不等式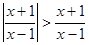 的解集是____ ____。
的解集是____ ____。 ,再朝新方向走了3千米,结果他离出发点恰好
,再朝新方向走了3千米,结果他离出发点恰好 千米,那么x的值是 。
千米,那么x的值是 。