题目内容
若AD是三角形ABC的中线，且|
|=6，|
|=6，|
|=4
，则边BC的长是 ．
| AB |
| AD |
| AC |
| 3 |
分析：根据题意画出相应的图形，如图所示，过A作AE垂直于BD，利用三线合一得到E为BD中点，设BC边长为4x，表示出AE与CE，利用余弦定理列出关于x的方程，求出方程的解得到x的值，即可确定出BC的长．
解答：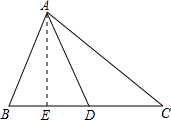
解：根据题意画出相应的图形，如图所示，过A作AE⊥BD，
∵|
|=|
|=6，∴|
|=|
|，
设|
|=4x，由D为边BC中点，得到|
|=x，|
|=2x，即|
|=3x，
|
|=
，
在△ACE中，根据余弦定理得：|
|2=|
|2+|
|2-2•
•
•cos∠AEC，
即48=36-x2+9x2，
解得：x=
，
则边BC长为2
．
故答案为：2
解：根据题意画出相应的图形，如图所示，过A作AE⊥BD，∵|
| AB |
| AD |
| BE |
| DE |
设|
| BC |
| DE |
| DC |
| EC |
|
| AE |
| 62-x2 |
在△ACE中，根据余弦定理得：|
| AC |
| AE |
| EC |
| AE |
| EC |
即48=36-x2+9x2，
解得：x=
| ||
| 2 |
则边BC长为2
| 6 |
故答案为：2
| 6 |
点评：此题考查了余弦定理，等腰三角形的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
（2013•南通一模）选修4-1：几何证明选讲
|＝6，|
|＝6，|
|＝4
，则边BC的长是________．
|=6，|
|=6，|
|=
，则边BC的长是 .