题目内容
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)(1)证明:P-ABC为正四面体;
(2)若PD=PA=
 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)(3)设棱台DEF-ABC的体积为V,是否存在体积为V且各棱长均相等的直平行六面体,使得它与棱台DEF-ABC有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.

【答案】分析:(1)利用已知条件证明DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°,从而证明P-ABC为正四面体;
(2)PD=PA= 取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角.
取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角.
解三角形DMA求二面角D-BC-A的大小;(结果用反三角函数值表示)
(3)存在满足条件的直平行六面体.设直平行六面体的棱长均为 ,底面相邻两边夹角为α,
,底面相邻两边夹角为α,
利用该六面体棱长和为6,体积为 sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求
sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求
解答: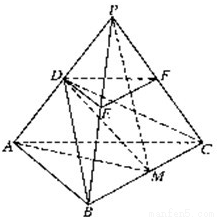 证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
∴DE+EF+FD=PD+OE+PF.
又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°,∴P-ABC是正四面体.
解:(2)取BC的中点M,连拉PM,DM.AM.
∵BC⊥PM,BC⊥AM,∴BC⊥平面PAM,BC⊥DM,
则∠DMA为二面角D-BC-A的平面角.
由(1)知,P-ABC的各棱长均为1,
∴PM=AM=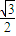 ,由D是PA的中点,得
,由D是PA的中点,得
sin∠DMA=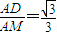 ,∴∠DMA=arcsin
,∴∠DMA=arcsin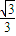 .
.
(3)存在满足条件的直平行六面体.
棱台DEF-ABC的棱长和为定值6,体积为V.
设直平行六面体的棱长均为 ,底面相邻两边夹角为α,
,底面相邻两边夹角为α,
则该六面体棱长和为6,体积为 sinα=V.
sinα=V.
∵正四面体P-ABC的体积是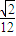 ,∴0<V<
,∴0<V<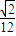 ,0<8V<1.可知α=arcsim(8V)
,0<8V<1.可知α=arcsim(8V)
故构造棱长均为 ,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
点评:本题考查棱柱、棱锥、棱台的体积,平面与平面平行的性质,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.
(2)PD=PA=
 取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角.
取BC的中点M,连拉PM,DM.AM.说明∠DMA为二面角D-BC-A的平面角.解三角形DMA求二面角D-BC-A的大小;(结果用反三角函数值表示)
(3)存在满足条件的直平行六面体.设直平行六面体的棱长均为
 ,底面相邻两边夹角为α,
,底面相邻两边夹角为α,利用该六面体棱长和为6,体积为
 sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求
sinα=V.求出α=arcsim(8V)底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求解答:
 证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
证明:(1)∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,∴DE+EF+FD=PD+OE+PF.
又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°,∴P-ABC是正四面体.
解:(2)取BC的中点M,连拉PM,DM.AM.
∵BC⊥PM,BC⊥AM,∴BC⊥平面PAM,BC⊥DM,
则∠DMA为二面角D-BC-A的平面角.
由(1)知,P-ABC的各棱长均为1,
∴PM=AM=
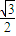 ,由D是PA的中点,得
,由D是PA的中点,得sin∠DMA=
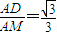 ,∴∠DMA=arcsin
,∴∠DMA=arcsin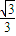 .
.(3)存在满足条件的直平行六面体.
棱台DEF-ABC的棱长和为定值6,体积为V.
设直平行六面体的棱长均为
 ,底面相邻两边夹角为α,
,底面相邻两边夹角为α,则该六面体棱长和为6,体积为
 sinα=V.
sinα=V.∵正四面体P-ABC的体积是
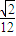 ,∴0<V<
,∴0<V<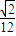 ,0<8V<1.可知α=arcsim(8V)
,0<8V<1.可知α=arcsim(8V)故构造棱长均为
 ,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.点评:本题考查棱柱、棱锥、棱台的体积,平面与平面平行的性质,二面角及其度量,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和) 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和) 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)
 PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA,求二面角D-BC-A的大小;(结果用反三角函数值表示) 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)