题目内容
已知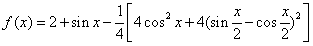 。
。
(Ⅰ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-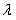 f(x)+1在[-
f(x)+1在[-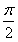 ,
,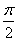 ]上是增函数,求实数
]上是增函数,求实数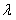 的取值范围。
的取值范围。
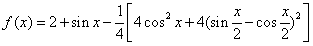 。
。(Ⅰ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-
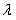 f(x)+1在[-
f(x)+1在[-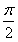 ,
,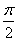 ]上是增函数,求实数
]上是增函数,求实数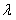 的取值范围。
的取值范围。 解: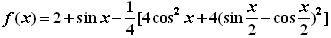
=2+sinx-cos2x-1+sinx=sin2x+2sinx,
(Ⅰ)设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y),
则x0=-x,y0=-y,
∵点M在函数y=f(x)的图象上,
∴-y=sin2(-x)+2sin(-x),即y=-sin2x+2sinx,
∴函数g(x)的解析式为g(x)=-sin2x+2sinx。
(Ⅱ)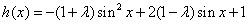 ,
,
设sinx=t,(-1≤t≤1),
则有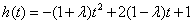 ,(-1≤t≤1)
,(-1≤t≤1)
①当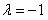 时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1;
时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1;
②当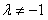 时,对称轴方程为直线
时,对称轴方程为直线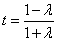 ,
,
ⅰ)λ<-1时,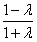 ≤-1,解得λ<-1;
≤-1,解得λ<-1;
ⅱ)λ>-1时,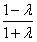 ≥1,解得-1<λ≤0,
≥1,解得-1<λ≤0,
综上,λ的取值范围是λ≤0。
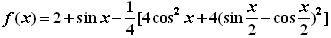
=2+sinx-cos2x-1+sinx=sin2x+2sinx,
(Ⅰ)设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y),
则x0=-x,y0=-y,
∵点M在函数y=f(x)的图象上,
∴-y=sin2(-x)+2sin(-x),即y=-sin2x+2sinx,
∴函数g(x)的解析式为g(x)=-sin2x+2sinx。
(Ⅱ)
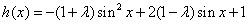 ,
,设sinx=t,(-1≤t≤1),
则有
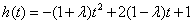 ,(-1≤t≤1)
,(-1≤t≤1)①当
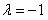 时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1;
时,h(t)=4t+1在[-1,1]上是增函数,∴λ=-1;②当
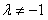 时,对称轴方程为直线
时,对称轴方程为直线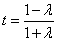 ,
,ⅰ)λ<-1时,
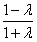 ≤-1,解得λ<-1;
≤-1,解得λ<-1;ⅱ)λ>-1时,
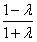 ≥1,解得-1<λ≤0,
≥1,解得-1<λ≤0,综上,λ的取值范围是λ≤0。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知全集U=R,若函数f(x)=x2-3x+2,集合M={x|f(x)≤0},N={x|f′(x)<0},则M∩CUN=( )
A、[
| ||
B、[
| ||
C、(
| ||
D、(
|