题目内容
数据5,7,7,8,10,11的标准差是
| A.8 | B.4 | C.2 | D.1 |
C
解析考点:极差、方差与标准差.
专题:计算题.
分析:先算出平均数,再根据方差公式计算方差,求出其算术平方根即为标准差.解答:解:这组数据的平均数. 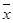 =(5+7+7+8+10+11)÷6=8,
=(5+7+7+8+10+11)÷6=8,
方差=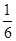 [(5-8)
[(5-8)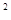 +(7-8)
+(7-8)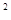 +(7-8)
+(7-8)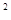 +(8-8)
+(8-8)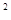 +(10-8)
+(10-8)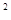 +(11-8)
+(11-8)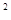 ]=4,
]=4,
标准差=2.
故选C.
点评:本题考查了标准差的求法,计算标准差需要先算出方差,计算方差的步骤是:(1)计算数据的平均数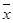 .
.
(2)再根据公式求出数据的方差.标准差即方差的算术平方根,注意标差和方差一样都是非负数.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
某中学有高级教师28人,中级教师54人,初级教师81人,为了调查他们的身体状况,从他们中抽取容量为36的样本,最适合抽取样本的方法是( )
| A.简单随机抽样 | B.系统抽样 | C.分层抽样 | D.先从高级教师中随机剔除1人,再用分层抽样 |
已知一组数据为20、30、40、50、60、60、70,则这组数据的众数、中位数、平均数的大小关系为( )
| A.中位数>平均数>众数 | B.平均数>众数>中位数 |
| C.众数>平均数>中位数 | D.众数>中位数>平均数 |
某单位有老、中、青职工43 0人,其中青年职工160人,中年职工是老职工的2倍,为了解职工身体状况,现采用分层抽样的方法进行调查,在抽出的样本中有青年职工32人,则该样本中老年职工人数为
0人,其中青年职工160人,中年职工是老职工的2倍,为了解职工身体状况,现采用分层抽样的方法进行调查,在抽出的样本中有青年职工32人,则该样本中老年职工人数为
| A.9 | B.18 | C.27 | D.36 |
已知变量 具有线性相关关系,且
具有线性相关关系,且 一组数据为
一组数据为 ,则回归方程为:
,则回归方程为:
A. | B. | C.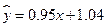 | D. |
从1008名学生中抽取20人参加义务劳动,规定采用下列方法选取:先用简单随机抽样的方法从1008人中剔除8人,剩下1000人再按系统抽样的方法抽取,那么在1008人中每人入选的概率是
| A.都相等且等于 | B.都相等且等于 | C.不全相等 | D.均不相等 |
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和; | B.残差平方和; |
| C.回归平方和; | D.相关指数R2. |