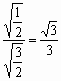题目内容
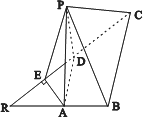
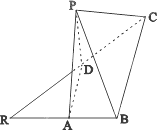
已知等腰Rt△RBC中,∠RBC=![]() ,RB=BC=2,点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD的位置,使PA⊥AB,连结PB、PC.
,RB=BC=2,点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD的位置,使PA⊥AB,连结PB、PC.
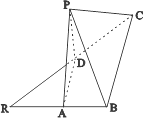
(1)求证:BC⊥PB;
(2)求二面角A-CD-P的平面角的余弦值.
答案:
解析:
解析:
|
解:(1)∵A、D分别为RB、RC的中点, ∴AD∥BC,∵∠RBC= ∴AD⊥RA,AD⊥PA. ∴AD⊥平面PAB ∴BC⊥平面PAB,PB ∴BC⊥PB. (2)∵PA⊥AB,∴PA⊥平面ABCD 过A作AE⊥RC于点E,连结PE,∴PE⊥RC. ∴PEA为二面角P-CD-A的平面角, ∵PA=1,BC=2,AE= ∴cos∠PEA= ∴二面角A-CD-P的平面角的余弦值为
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目