题目内容
(12分)已知函数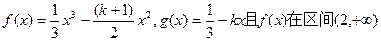 上为增函数.
上为增函数.
(1)求k的取值范围;
(2)若函数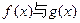 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
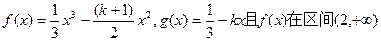 上为增函数.
上为增函数.(1)求k的取值范围;
(2)若函数
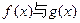 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.k≤1,

21解:(1)由题意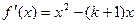 ……………………1分
……………………1分
因为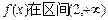 上为增函数,所以
上为增函数,所以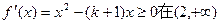 上恒成立,…3分
上恒成立,…3分
即 ,所以
,所以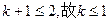 ……………………4分
……………………4分
当k=1时,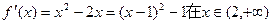 恒大于0,故
恒大于0,故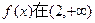 上单增,符合题意.
上单增,符合题意.
所以k的取值范围为k≤1.……………………5分
(2)设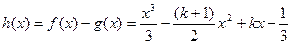 ,
,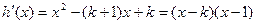
令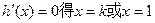 ………………7分
………………7分
由(1)知k≤1,
①当k=1时,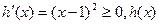 在R上递增,显然不合题意………8分
在R上递增,显然不合题意………8分
②当k<1时,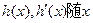 的变化情况如下表:
的变化情况如下表:
……………………10分
由于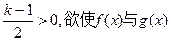 图象有三个不同的交点,即方程
图象有三个不同的交点,即方程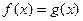 ,
,
也即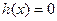 有三个不同的实根。故需
有三个不同的实根。故需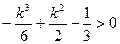 即
即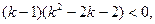
所以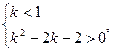 解得
解得 。综上,所求k的范围为
。综上,所求k的范围为 .……………………12分
.……………………12分
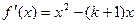 ……………………1分
……………………1分因为
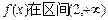 上为增函数,所以
上为增函数,所以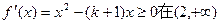 上恒成立,…3分
上恒成立,…3分即
 ,所以
,所以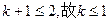 ……………………4分
……………………4分当k=1时,
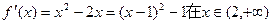 恒大于0,故
恒大于0,故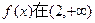 上单增,符合题意.
上单增,符合题意.所以k的取值范围为k≤1.……………………5分
(2)设
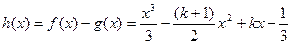 ,
,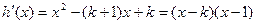
令
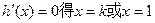 ………………7分
………………7分由(1)知k≤1,
①当k=1时,
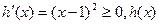 在R上递增,显然不合题意………8分
在R上递增,显然不合题意………8分②当k<1时,
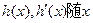 的变化情况如下表:
的变化情况如下表:| x | 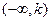 | k | (k,1) | 1 | (1,+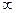 ) ) |
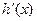 | + | 0 | - | 0 | + |
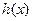 | ↗ | 极大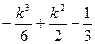 | ↘ | 极小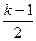 | ↗ |
由于
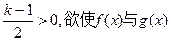 图象有三个不同的交点,即方程
图象有三个不同的交点,即方程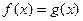 ,
,也即
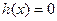 有三个不同的实根。故需
有三个不同的实根。故需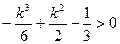 即
即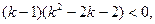
所以
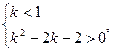 解得
解得 。综上,所求k的范围为
。综上,所求k的范围为 .……………………12分
.……………………12分
练习册系列答案
相关题目
 )试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
)试将利润y表示为x的函数,并求出上涨几元,可获最大利润. 知函数
知函数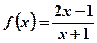
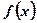 的定义域;
的定义域;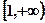 上是减函数.
上是减函数.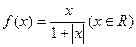 时,分别给出下面四个结论:
时,分别给出下面四个结论: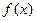 的图象关于
的图象关于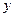 轴对称;② 函数
轴对称;② 函数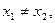 则一定有
则一定有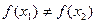 ;④若规定
;④若规定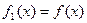 ,
, 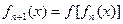 ,则
,则 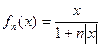 对任意
对任意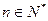 恒成立. 你认为上述四个结论中正确的有
恒成立. 你认为上述四个结论中正确的有 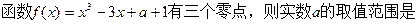 ;
;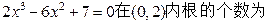 ( )
( )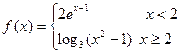 ,则不等式
,则不等式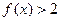 的解集为 ( )
的解集为 ( )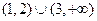
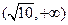
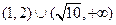
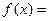
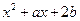 的两个根分别在(0,1),(1,2)内,则
的两个根分别在(0,1),(1,2)内,则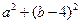 的取值范围为( )
的取值范围为( )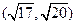
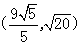
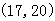
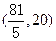
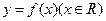 ,满足
,满足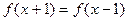 ,且
,且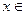 [
[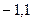 ],
],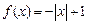 ,则
,则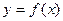 与
与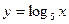 的图像的交点的个数为 ( )
的图像的交点的个数为 ( ) 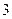 个
个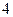 个
个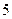 个
个 个
个