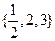题目内容
陈老师购买安居工程的集资房92平方米,单价为?1 000?元/平方米,一次性国家财政补贴28 800元,学校补贴14 400元,余款由个人负担.房地产开发公司对教师实行分期付款(注①),每期为1年,等额付款,签订购房合同后1年付款1次,再经过1年又付款1次,共付10次,10年后付清,如果按年利率7.5%,每年按复利计算(注②),那么每年应付款多少元?画出程序框图,并写出计算所需的程序.(计算结果精确到百元)(注③)
注:①分期付款,各期所付的款以及最后1次付款时所生的利息合计应等于个人负担的购房余款的现价及这个房款现价到最后1次付款时所生的利息之和.
②每年按复利计算,即本年利息计入次年的本金生息.
③必要时参考下列数据:
1.0759≈1.917,1.07510≈2.061,1.07511≈2.216.
注:①分期付款,各期所付的款以及最后1次付款时所生的利息合计应等于个人负担的购房余款的现价及这个房款现价到最后1次付款时所生的利息之和.
②每年按复利计算,即本年利息计入次年的本金生息.
③必要时参考下列数据:
1.0759≈1.917,1.07510≈2.061,1.07511≈2.216.
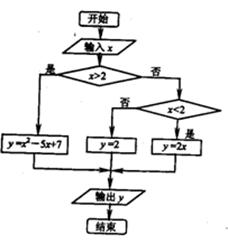
解:程序框图如下图所示

程序如下:
i=1;
s=0;
x=0;
m=1;
a="48" 800;
while i<=10
s=s+m;
m=m*1.075;
i=i+1;
end
x=a*m/s;
print(%io(2),x);
设每年应付款x元,那么到最后1次付款时(即购买10年后),
第1年付款及所生利息之和为x×1.0759元,
第2年付款及所生利息之和为x×1.0758元,
……
第9年付款及所生利息之和为x×1.075元,
第10年付款为x元,
而所购房余款的现价及其利息之和为[1 000×92-(28 800+14 400)]×1.07510="48" 800×1.07510(元).
因此有x(1+1.075+1.0752+…+1.0759)="48" 800×1.07510(元).
x="7" 109.473 3.
第1年付款及所生利息之和为x×1.0759元,
第2年付款及所生利息之和为x×1.0758元,
……
第9年付款及所生利息之和为x×1.075元,
第10年付款为x元,
而所购房余款的现价及其利息之和为[1 000×92-(28 800+14 400)]×1.07510="48" 800×1.07510(元).
因此有x(1+1.075+1.0752+…+1.0759)="48" 800×1.07510(元).
x="7" 109.473 3.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 当
当 时的函数值时.
时的函数值时. 的值为( )
的值为( )
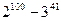 的个位数是
的个位数是  在x=5时所对应的
在x=5时所对应的 的值为( )
的值为( ) ,
, )
)
 }
}