题目内容
我们将点P（x，y）经过矩阵
的变换得到新的点P'（x'，y'）称作一次运动，即：
=
．
（1）若点P（3，4）经过矩阵A=
变换后得到新的点P'，求出点P'的坐标，并指出点P'与点P的位置关系；
（2）若函数f(x)=
x2+
（x≥0）的图象上的每一个点经过（1）中的矩阵A变换后，所得到图象对应函数y=g（x），试研究在y=g（x）上是否存在定义域与值域相同的区间[m，n]，若存在，求出满足条件的实数a的取值范围；若不存在，说明理由．
|
|
|
|
（1）若点P（3，4）经过矩阵A=
|
（2）若函数f(x)=
| 1 |
| a |
| 5 |
| a |
（1）∵
=
，∴P'的坐标为（4，3）（2分）
显然点P'与点P关于直线y=x成轴对称；（4分）
（2）由（1）知y=g（x）为y=f（x）的反函数，（5分）
∴x2=ay-5，∴x=
∴当a＞0时，g(x)=
（x≥
）（7分）
当a＜0时，g(x)=
（x≤
）（8分）
当a＞0时，函数y=g（x）在定义域内单调递增，
要使函数y=g（x）存在定义域与值域相同的区间[m，n]，
只需方程
=x当x≥0时有两个相异实根，（10分）
即方程ax-5=x2有两个相异正根（x=0显然不是方程的根），∴a=x+
（x＞0）即函数y=a与函数y=x+
（x＞0）有两个交点，
由基本不等式可知：a＞2
（x+
≥2
当且仅当x=
时有最小值）（12分）
当a＜0时，∵函数y=g（x）的值域为[0，+∞），而x≤
＜0，∴当a＜0时，不存在定义域与值域相同的区间[m，n]，∴a的取值范围为(2
，+∞)．（14分）
|
|
|
显然点P'与点P关于直线y=x成轴对称；（4分）
（2）由（1）知y=g（x）为y=f（x）的反函数，（5分）
∴x2=ay-5，∴x=
| ay-5 |
| ax-5 |
| 5 |
| a |
当a＜0时，g(x)=
| ax-5 |
| 5 |
| a |
当a＞0时，函数y=g（x）在定义域内单调递增，
要使函数y=g（x）存在定义域与值域相同的区间[m，n]，
只需方程
| ax-5 |
即方程ax-5=x2有两个相异正根（x=0显然不是方程的根），∴a=x+
| 5 |
| x |
| 5 |
| x |
由基本不等式可知：a＞2
| 5 |
| 5 |
| x |
| 5 |
| 5 |
当a＜0时，∵函数y=g（x）的值域为[0，+∞），而x≤
| 5 |
| a |
| 5 |
练习册系列答案
相关题目
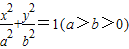（如图），求证：xE•xF是与MN和点P位置无关的定值；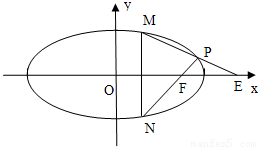
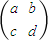的变换得到新的点P'（x'，y'）称作一次运动，即：
．
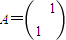变换后得到新的点P'，求出点P'的坐标，并指出点P'与点P的位置关系；
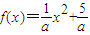（x≥0）的图象上的每一个点经过（1）中的矩阵A变换后，所得到图象对应函数y=g（x），试研究在y=g（x）上是否存在定义域与值域相同的区间[m，n]，若存在，求出满足条件的实数a的取值范围；若不存在，说明理由．
（如图），求证：xE•xF是与MN和点P位置无关的定值；