题目内容
19、为赢得2010年广州亚运会的商机，某商家最近进行了新科技产品的市场分析，调查显示，新产品每件成本9万元，售价为30万元，每星期卖出432件，如果降低价格，销售量可以增加，且每星期多卖出的商品件数与商品单价的降低值0≤x≤30（单位：万元，0≤x≤30）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．
（1）将一个星期的商品销售利润表示成f（x）的函数；
（2）如何定价才能使一个星期的商品销售利润最大？
（1）将一个星期的商品销售利润表示成f（x）的函数；
（2）如何定价才能使一个星期的商品销售利润最大？
分析：（1）一个星期的商品销售利润=（每件商品售价-降低价-成本价）×卖出数量，依此建立函数关系式；
（2）由（1）知，f（x）是一元三次函数，求它在闭区间上的最值，要用求导法．
（2）由（1）知，f（x）是一元三次函数，求它在闭区间上的最值，要用求导法．
解答：解：（1）设商品降价x万元，则多卖的商品数为kx2，
若记商品在一个星期的获利为f（x），
则依题意，有f（x）=（30-x-9）（432+kx2）=（21-x）（432+kx2），
又，由已知条件：24=k•22，得 k=6，
所以，f（x）=-6x3+126x2-432x+9072，x∈[0，30]．
（2）根据（1），得 f'（x）=-18x2+252x-432=-18（x-2）（x-12）
作出以下表格：
所以，当x=12时，f（x）达到极大值．因为f（0）=9072，f（12）=11264，
即定价为 30-12=18万元时，能使一个星期的商品销售利润最大．
若记商品在一个星期的获利为f（x），
则依题意，有f（x）=（30-x-9）（432+kx2）=（21-x）（432+kx2），
又，由已知条件：24=k•22，得 k=6，
所以，f（x）=-6x3+126x2-432x+9072，x∈[0，30]．
（2）根据（1），得 f'（x）=-18x2+252x-432=-18（x-2）（x-12）
作出以下表格：
| x | [0，2） | 2 | （2，12） | 12 | （12，30] |
| f'（x） | - | 0 | + | 0 | - |
| f（x） | ↘ | 极小 | ↗ | 极大 | ↘ |
即定价为 30-12=18万元时，能使一个星期的商品销售利润最大．
点评：本题考查了由函数模型建立目标函数，利用求导法求三次函数在闭区间上的最值问题，是中档题．
练习册系列答案
字词句段篇系列答案
相关题目
量可以增加，且每星期多卖出的商品件数与商品单价的降低值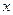
（单位：万元，
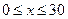）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．（1）将一个星期的商品销售利润表示成
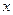（单位：万元，
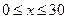）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．（1）将一个星期的商品销售利润表示成
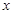（单位：万元，
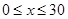）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．（1）将一个星期的商品销售利润表示成
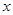（单位：万元，
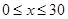）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．（1）将一个星期的商品销售利润表示成