题目内容
(08年浙江卷理)(本题15分)已知![]() 是实数,函数
是实数,函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() 为
为![]() 在区间
在区间![]() 上的最小值.
上的最小值.
(i)写出![]() 的表达式;
的表达式;
(ii)求![]() 的取值范围,使得
的取值范围,使得![]() .
.
本题主要考查函数的性质、求导、导数的应用等基础知识,同时考查分类讨论思想
以及综合运用所学知识分析问题和解决问题的能力.满分15分.
(Ⅰ)解:函数的定义域为![]() ,
,![]() (
(![]() ).
).
若![]() ,则
,则![]() ,
,![]() 有单调递增区间
有单调递增区间![]() .
.
若![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
![]() 有单调递减区间
有单调递减区间![]() ,单调递增区间
,单调递增区间![]() .
.
(Ⅱ)解:(i)若![]() ,
,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
若![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .
.
若![]() ,
,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.
综上所述,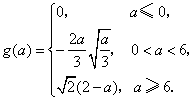
(ii)令![]() .
.
若![]() ,无解.
,无解.
若![]() ,解得
,解得![]() .
.
若![]() ,解得
,解得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
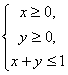 时,恒有
时,恒有