题目内容
在棱长为a的正方体骨架内放置一气球,使其充气且尽可能地膨胀(仍保持为球的形状),则气球表面积的最大值为 .
【答案】分析:由题意气球充气且尽可能地膨胀(仍保持为球的形状),与棱长为a的正方体框架相切,球的直径就是正方体面对角线的一半.求出半径,即可求出球的表面积.
解答: 解:气球充气且尽可能地膨胀(仍保持为球的形状),
解:气球充气且尽可能地膨胀(仍保持为球的形状),
与棱长为a的正方体框架相切,球的直径就是正方体面对角线的一半.
所以球的直径为: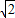 a,半径为:
a,半径为:
气球表面积的最大值:4πr2=2πa2
故答案为:2πa2.
点评:本小题主要考查球的体积和表面积、正方体等基础知识,考查运算求解能力,考查逻辑思维能力.属于基础题.
解答:
 解:气球充气且尽可能地膨胀(仍保持为球的形状),
解:气球充气且尽可能地膨胀(仍保持为球的形状),与棱长为a的正方体框架相切,球的直径就是正方体面对角线的一半.
所以球的直径为:
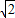 a,半径为:
a,半径为:
气球表面积的最大值:4πr2=2πa2
故答案为:2πa2.
点评:本小题主要考查球的体积和表面积、正方体等基础知识,考查运算求解能力,考查逻辑思维能力.属于基础题.

练习册系列答案
相关题目