题目内容
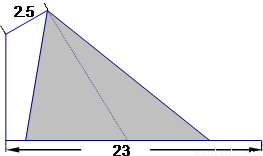
 在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)(
在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)(| 3 |
分析:记灯柱顶端为B,灯罩顶为A,灯杆为AB,灯罩轴线与道路中线交于C,以灯柱底端O点为原点,灯柱OB所在直线为y轴,路宽OC所在直线为x轴,建立如图所示的直角坐标系,求出AC的方程,即可求得结论.
解答:解:记灯柱顶端为B,灯罩顶为A,灯杆为AB,灯罩轴线与道路中线交于C,以灯柱底端O点为原点,灯柱OB所在直线为y轴,路宽OC所在直线为x轴,建立如图所示的直角坐标系,
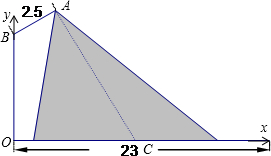
则B点的坐标为(0,h),C点的坐标为(11.5,0))
因为灯杆AB与灯柱OB成120°角,所以AB的倾斜角为30°,则A点的坐标为(2.5cos30°,h+2.5sin30°),
即(1.25
,h+1.25)
因为CA⊥BA,所以kAC=-
=-
,
由点斜式得CA的方程为y-(h+1.25)=-
(x-1.25
),
因为灯罩轴线CA过点C(11.5,0),所以0-(h+1.25)=-
(11.5-1.25
),
所以h≈14.92(米)

则B点的坐标为(0,h),C点的坐标为(11.5,0))
因为灯杆AB与灯柱OB成120°角,所以AB的倾斜角为30°,则A点的坐标为(2.5cos30°,h+2.5sin30°),
即(1.25
| 3 |
因为CA⊥BA,所以kAC=-
| 1 |
| kAB |
| 3 |
由点斜式得CA的方程为y-(h+1.25)=-
| 3 |
| 3 |
因为灯罩轴线CA过点C(11.5,0),所以0-(h+1.25)=-
| 3 |
| 3 |
所以h≈14.92(米)
点评:本题考查直线方程的确定与运用,解题的关键是建立坐标系,确定点的坐标.

练习册系列答案
相关题目
 在路边安装路灯,灯柱OA的高为h,路宽OC为23米,灯杆AB的长为2.5米,且与灯柱OA成120°角.路灯采用锥形灯罩,灯罩轴线BD与灯杆AB垂直.请你建立适当的直角坐标系,解决以下问题:
在路边安装路灯,灯柱OA的高为h,路宽OC为23米,灯杆AB的长为2.5米,且与灯柱OA成120°角.路灯采用锥形灯罩,灯罩轴线BD与灯杆AB垂直.请你建立适当的直角坐标系,解决以下问题: 在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)(
在路边安装路灯,路宽23m,灯杆长2.5m,且与灯柱成120°角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)( )
) )
)
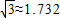 )
)