题目内容
（09年丰台区期末理）（13分）
已知向量
=
,
=
，且x∈
。
（Ⅰ）求?及|?|；
（Ⅱ）若f ( x ) = ?
|?|的最小值为
，且
∈
，求的值。
解析：（Ⅰ）
?
=
= cos2x ……………………… 2分
|+| =
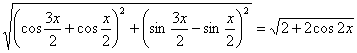… 5分
因为 x∈
，所以 cosx
0 所以|+| = 2cos x ………… 6分
（Ⅱ）f ( x ) =? 2
|+| = 2cos x 4cos x = 2 cos2x 4cos x 1
= 2 ( cos x )2 1 22 ……………………………… 8分
令t = cos x∈[ 0 , 1 ]，则f ( x ) = g ( t ) = 2 ( t )2 1 22
①当0
1时，当且仅当t =时，f ( x )取得最小值，
g () = 1 22 即 1 22兴=
=
………… 10分
②当＞1时，当且仅当t = 1时，f ( x )取得最小值，g ( 1 ) = 1 4
即1 4=
＜1不合题意，舍去。……………………… 12分
=………………………………………………………… 13分 
练习册系列答案
阅读快车系列答案
相关题目
(a＞b＞0)的离心率为
，长轴长为
，设过右焦点F倾
的直线交椭圆M于A，B两点。
；
? 3ax 4x的义域为[0，1]。