题目内容
已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=∅,求实数m的取值范围.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=∅,求实数m的取值范围.
(1)(-∞,3] (2)254 (3)(-∞,2)∪(4,+∞)
解:(1)因为A∪B=A,所以B⊆A,当B=∅时,m+1>2m-1,则m<2;
当B≠∅时,根据题意作出如图所示的数轴,可得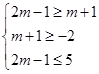 ,解得2≤m≤3.
,解得2≤m≤3.
综上可得,实数m的取值范围是(-∞,3].
(2)当x∈Z时,A={x|-2≤x≤5}={-2,-1,0,1,2,3,4,5},共有8个元素,所以A的非空真子集的个数为28-2=254.
(3)当B=∅时,由(1)知m<2;当B≠∅时,根据题意作出如图所示的数轴,
可得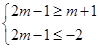 ,
,
或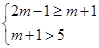 ,解得m>4.
,解得m>4.
综上可得,实数m的取值范围是(-∞,2)∪(4,+∞).
当B≠∅时,根据题意作出如图所示的数轴,可得
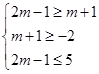 ,解得2≤m≤3.
,解得2≤m≤3.综上可得,实数m的取值范围是(-∞,3].
(2)当x∈Z时,A={x|-2≤x≤5}={-2,-1,0,1,2,3,4,5},共有8个元素,所以A的非空真子集的个数为28-2=254.

(3)当B=∅时,由(1)知m<2;当B≠∅时,根据题意作出如图所示的数轴,
可得
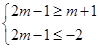 ,
,或
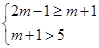 ,解得m>4.
,解得m>4.综上可得,实数m的取值范围是(-∞,2)∪(4,+∞).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
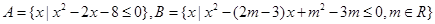
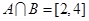 ,求实数m的值;
,求实数m的值;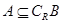 ,求实数m的取值范围。
,求实数m的取值范围。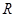 ,
,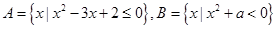 .
.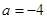 时,求
时,求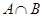 和
和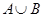 ;
;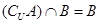 ,求实数
,求实数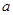 的取值范围.
的取值范围. x+1,x∈[
x+1,x∈[ ,2]},B={x|x+m2≥1};命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.
,2]},B={x|x+m2≥1};命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.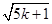 ,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.
,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.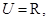 集合
集合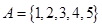 ,
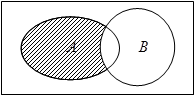
,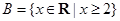 ,下图中阴影部分所表示的集合为( )
,下图中阴影部分所表示的集合为( )
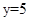
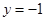
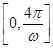
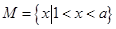 ,
,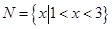 ,则“
,则“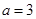 ”是“
”是“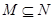 ”的( )
”的( )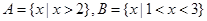 ,则
,则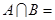 ( )
( )


