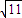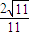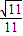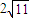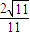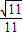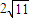题目内容
(理)已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2,点B到平面EFG的距离为( )
A.
| B.
| C.
| D.2
|
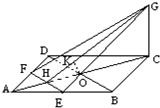
如图,连接EG、FG、EF、BD、AC、EF、BD分别交AC于H、O.
因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
由直线和平面平行的判定定理知BD∥平面EFG,所以BD和平面EFG的距离就是点B到平面EFG的距离.
∵BD⊥AC,∴EF⊥HC.
∵GC⊥平面ABCD,∴EF⊥GC,
∵HC∩GC=C,∴EF⊥平面HCG.
∵EF?平面EFG,∴平面EFG⊥平面HCG,HG是这两个垂直平面的交线.
作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离.
∵正方形ABCD的边长为4,GC=2,
∴AC=4
| 2 |
| 2 |
| 2 |
∴在Rt△HCG中,HG=
| 18+4 |
| 22 |
由于Rt△HKO和Rt△HCG有一个锐角是公共的,故Rt△HKO∽△HCG.
∴OK=
| HO?GC |
| HG |
| ||
|
2
| ||
| 11 |
即点B到平面EFG的距离为
2
| ||
| 11 |
故选B.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 B.
B.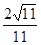 C.
C.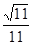 D.
D.