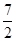题目内容
已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面积之和,则该正四棱台的高是( )
分析:利用棱台的高、斜高、边心距构成直角梯形,通过构造直角三角形,利用勾股定理求出正四棱台的高.
解答:解:设正四棱台的高为h,斜高为x,由题意可得 4•
•(3+6)x=32+62,∴x=
.
再由棱台的高、斜高、边心距构成直角梯形、可得 h=
=2,
故选A.
| 1 |
| 2 |
| 5 |
| 2 |
再由棱台的高、斜高、边心距构成直角梯形、可得 h=
x2-(
|
故选A.
点评:本题主要考查正四棱台的结构特征,利用了棱台的高、斜高、边心距构成直角梯形,通过构造直角三角形,利用勾股定理求出正四棱台的高,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
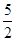 C.3 D.
C.3 D.